[ 2009 Mock Exam (PM) ] Derivative Investments .Questions 49-54

Tarja Stahlberg Case Scenario
Tarja Stahlberg, the company treasurer for the Finnish-based Borealis Group Oyj, is planning to repatriate ?100 million from its British subsidiary. She intends to convert the British pounds to euros (the home currency for Borealis) in 90 days. Nicholas Howell is advising Stahlberg on these transactions. Stahlberg has told Howell that she wants to protect Borealis against the possibility that the British pound depreciates against the euro before the funds are repatriated.
Howell suggests that Stahlberg consider the use of foreign currency options. In particular, a European call option on euros will allow Borealis to hedge its foreign currency risk. Howell makes the following statements:
Statement 1: “The call option price will decrease as the time to expiration decreases or the exercise price decreases; and is very sensitive to the risk-free rate.
Statement 2: You can use 90-day call options on the euro with a strike price of ?0.6400. The current 90-day forward exchange rate is ?0.6500. A synthetic European call option on the euro can be created by combining a long put position on the euro, a short position in a forward contract on the euro, and a short position in a zero-coupon bond.” Stahlberg mentions that Borealis will have ongoing U.S. dollar borrowing needs, and that she wants to use the Eurodollar market to meet these. She prefers to use floating rate debt, and is considering issuing a U.S. dollar denominated floating rate note (FRN). Stahlberg is concerned that an increase in U.S. yields before the FRN issuance date will increase her future borrowing costs (measured in U.S. dollars).
Howell explains how swaps and swaptions can be used to address Stahlberg’s concerns, stating: Statement 3: “Similar to a forward contract, a plain vanilla interest rate swap can fix borrowing costs. For example, if you issued a US$100 million FRN today that has a 180-day term and coupon payments that reset every 90 days at the 90-day LIBOR, a plain vanilla interest rate swap could convert it to a fixed rate obligation.
Statement 4: A newly entered plain vanilla interest rate swap has no current credit risk, but has potential credit risk that will increase steadily over the life of the swap.
Statement 5: A receiver swaption permits the holder to enter into a pay floating position and is equivalent to a put option.
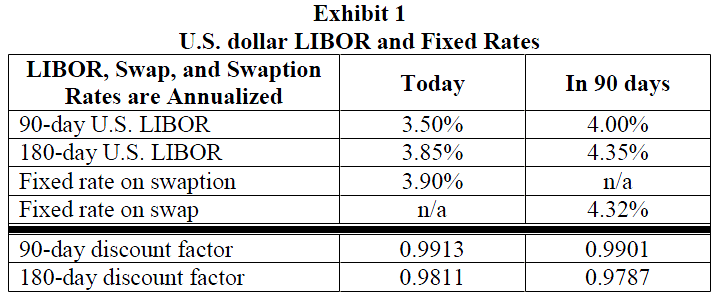
Statement 6: Suppose that you planned to issue a US$100 million FRN in 90 days time that has a 180-day term and coupon payments that reset every 90 days at the 90-day LIBOR. You would want a European swaption with a notional principal amount of US$100 million and a 90-day expiry at the time of FRN issuance. The data for this example is presented in Exhibit 1.


49. The information in Statement 1 is correct with respect to:

A. exercise price.
B. time to expiration.
C. risk-free interest rate.

Answer: B
“Option Markets and Contracts”, Don M. Chance 2009 Modular Level II, Volume 6, pp.195-197 Study Session 17-62-d Explain how an option price, as presented by the Black-Scholes-Merton model, is affected by each of the input values (the option Greeks). As expiration approaches, the price of the option moves toward the payoff value of the option at expiration, a process known as time value decay.

50. Statement 2 is incorrect with respect to which position?

A. put option

B. forward contract
C. zero-coupon bond

Answer: B
“Option Markets and Contracts”, Don M. Chance
2009 Modular Level II, Volume 6, pp. 202-205 Study Session17-62-i Illustrate how put-call parity for options on forwards (or futures) is established.
A synthetic call option is constructed by being long a forward, long the put option, and long or short a zero-coupon bond. Since Howell stated that F(0,T) > X, then this would be a short position in the zero-coupon bond.

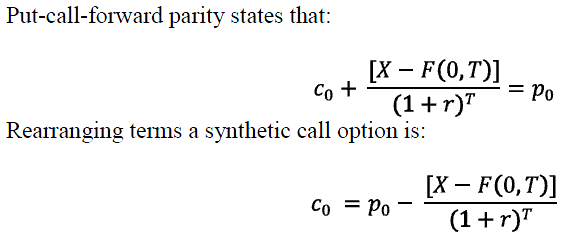
That is you take a long position in the put, a short bond position and a long forward position.

51. Given the information in Statement 3 and Exhibit 1, the annualized fixed rate on the plain vanilla interest rate swap would be closest to:

A. 1.76%.
B. 3.84%.
C. 4.32%.

Answer: B
“Swap Markets and Contracts”, Don M. Chance 2009 Modular Level II, Volume 6, pp. 240-244 Study Session 17-63-c Calculate and interpret the fixed rate on a plain vanilla interest rate swap and the market value of the swap during its life.



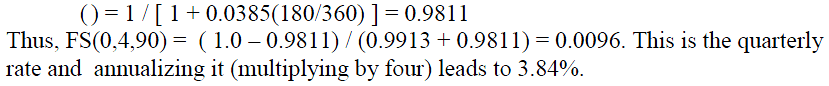
52. Statement 4 can be best characterized as:

A. correct with respect to current credit risk only.
B. correct with respect to potential credit risk only.
C. correct with respect to both current credit risk and potential credit risk.

Answer: A
“Swap Markets and Contracts”, Don M. Chance
2009 Modular Level II, Volume 6, pp. 262-263 Study Session17-63-i Evaluate swap credit risk for each party and over the life of the swap, distinguish between
current credit risk and potential credit risk, and illustrate how swap credit risk is reduced by both netting and marking to market. While there is no credit risk at contract initiation, the potential credit risk of an interest rate swap is greatest at the middle of its life; it does not increase throughout the life of the swap.

53. Statement 5 is can be best characterized as:

A. incorrect with respect to the pay floating position.
B. incorrect with respect to the put option equivalency.
C. correct with respect to both put option equivalency and pay floating position.

Answer: B
“Swap Markets and Contracts”, Don M. Chance
2009 Modular Level II, Volume 6, pp.256-257 Study Session 17-63-f Explain and interpret the characteristics and uses of swaptions, including the difference between payer and receiver swaptions.
A receiver swaption is equivalent to a call option.

54. Based on Statement 6 and Exhibit 1, the market value of the swaption at expiration would be closest to:

A. $206,725.
B. $207,764.
C. $208,961.

Answer: A
“Swap Markets and Contracts”, Don M. Chance
2009 Modular Level II, Volume 6, pp. 260-262 Study Session 17-63-h Calculate and interpret the value of an interest rate swaption on the expiration day The payoff of a payer swap in which the exercise price is x and the market rate on the underlying swap is FS(0,n,m) is: Max[0, FS(0,n,m) – x] *?j (hj)
Using the information in Exhibit 1 and Howell’s sixth statement:
[4.32% - 3.90%) * (90/360)]= $105,000
( ) = 1 / ( 1 + 0.0400*90/360) = 0.9901 ( ) = 1 / ( 1 + 0.0435*180/360) = 0.9787 ($105,000 * 0.9901) + ($105,000 * 0.9787)