Jacques Nordique Case Scenario
Jacques Nordique is a quantitative analyst at Brimford Investment Management. One of the firm’s managing partners asks Nordique to collect and analyze data as part of a project to explain and to forecast the behavior of price/earnings (P/E) ratios. Nordique wants to examine timeseries models of P/E behavior and begins by collecting 15 years of monthly data on market P/E ratios.
After considering several different time-series models, Nordique estimates a regression equation of the form:
(P/E)t = b0 + b1 (P/E)t–1 + εt Equation 1
and obtains the results shown in Exhibit 1. Nordique believes the time series is mean reverting and given the estimated coefficients, he calculates the mean-reverting level of the market P/E ratio to be 13.3.
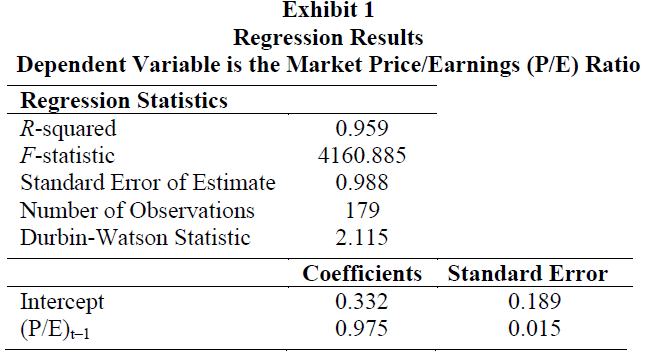
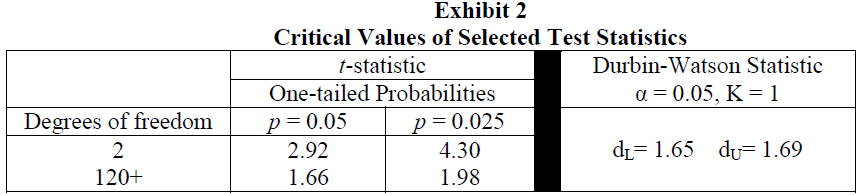
Nordique shares his time-series results with his supervisor, Amy Beloit. She is interested in the implications for stock-bond allocation, especially given that Brimford’s investment strategists are neutral on the future direction of interest rates. After reviewing the results, Beloit has two concerns about the time series estimated in Exhibit 1: (1) do the error terms exhibit heteroskedasticity; and (2) does the time series exhibit a unit root? Exhibit 2 contains critical values of several test statistics that may be relevant to the results that Nordique and Beloit are interpreting.
7. Nordique’s most appropriate action to determine if Equation 1 correctly fits the time series is to examine the:
A. R-squared value and F-statistic.
B. autocorrelation between the error terms.
C. correlation between the squared error terms and the independent variable.
Answer: B
“Time Series Analysis,” Richard A. DeFusco, CFA, Dennis W. McLeavey, CFA, Jerald E.
Pinto, CFA, and David E. Runkle, CFA 2009 Modular Level II, Volume 1, pp. 374-379 Study Session 3-13-d Discuss the structure of an autoregressive model of order p, calculate one- and two-period- ahead forecasts given the estimated coefficients, and explain how autocorrelations of the residuals can be used to test whether the autoregressive model fits the time series.
Testing for correct specification of an autoregressive (AR) model requires a test to determine if the correlations between the error term and several lagged error terms are statistically different from zero. If the autocorrelations are significantly different from zero, the model is not correctly specified.
8. To determine whether Beloit’s first concern is valid, Nordique’s most appropriate action would be to:
A. perform the Dickey-Fuller test.
B. regress the squared residuals from Equation 1 on the squared residuals lagged one period.
C. test whether the variance of the error in one period depends on the variance of the error in successive time periods.
Answer: B
“Time Series Analysis,” Richard A. DeFusco, CFA, Dennis W. McLeavey, CFA, Jerald E. Pinto, CFA, and David E. Runkle, CFA
2009 Modular Level II, Volume 1, pp. 407-410 Study Session 3-13-l Explain autoregressive conditional heteroskedasticity (ARCH), and discuss how ARCH models can be applied to predict the variance of a time series.
To examine for the presence of heteroskedasticity, Nordique should test whether the variance of the error in one period depends on the variance of the error in previous periods. This is accomplished by regressing the squared residuals from the estimated model on the squared residuals lagged one period.
9. Which of the following models is most appropriate to determine if Beloit’s second concern is justified?
A. (P/E)t – (P/E)t–1 = b0 + g1 (P/E)t–1 + εt
B. (P/E)t – (P/E)t–1 = b0 + g1 [(P/E)t – (P/E)t–1] + εt
C. (P/E)t – (P/E)t–1 = b0 + g1 [(P/E)t–1 – (P/E)t–2] + εt
Answer: A
“Time Series Analysis,” Richard A. DeFusco, CFA, Dennis W. McLeavey, CFA, Jerald E.
Pinto, CFA, and David E. Runkle, CFA 2009 Modular Level II, Volume 1, pp. 388-396 Study Session 3-13-i, j Discuss the implications of unit roots for time-series analysis, explain when unit roots are likely to occur and how to test for them, and demonstrate how a time series with a unit root can be transformed so that it can be analyzed with an autoregressive model. Discuss the steps of the unit root test for nonstationarity, and explain the relation of the test to autoregressive time series models.
The Dickey-Fuller test is used to test for the presence of a unit root. The model is of the form: (P/E)t – (P/E)t–1 = b0 + g1 (P/E)t–1 + εt. The null hypothesis (H0: g1 = 0) is that the series has a unit root and is not stationary. The alternate hypothesis (H1: g1 ≠ 0) is that the series does not have a unit root and is stationary.
10. If Beloit’s second concern about the time-series results in Exhibit 1 is correct, Nordique’s most appropriate action is to:
A. do nothing.
B. re-estimate the regression using the form: (P/E)t
C. re-estimate the regression using the form: [(P/E)t = b0 + b1 (P/E)t-1 + b2 (P/E)t-2 + εt.
Answer: C
– (P/E)t-1 ] = b0 + b1 [(P/E)t-1 – (P/E)t-2 ] + εt.
“Time Series Analysis,” Richard A. DeFusco, CFA, Dennis W. McLeavey, CFA, Jerald E. Pinto, CFA, and David E. Runkle, CFA 2009 Modular Level II, Volume 1, pp. 388-392 Study Session 3-13-i Discuss the implications of unit roots for time-series analysis, explain when unit roots are likely to occur and how to test for them, and demonstrate how a time series with a unit root can be transformed so that it can be analyzed with an autoregressive model. Beloit is concerned that a unit root exists. If she is correct, first differencing is a suggested solution, i.e., re-estimate the regression using the form: [(P/E)t
11. If Nordique’s belief about the behavior of the time series is correct, which of the following is most appropriate? – (P/E)t-1 ] = b0 + b1 [(P/E)t-1 – (P/E)t-2 ] + εt.
A. Underweight stocks if the P/E is above its historical average.
B. Overweight stocks if the P/E is above its mean reversion level.
C. Underweight stocks if the P/E is above its mean reversion level.
Answer: C
“Time Series Analysis,” Richard A. DeFusco, CFA, Dennis W. McLeavey, CFA, Jerald E. Pinto, CFA, and David E. Runkle, CFA 2009 Modular Level II, Volume 1, p. 379
Study Session 3-13-e Explain mean reversion, and calculate a mean-reverting level.
If the process is mean reverting, the market P/E will move toward the mean-reverting level over time. If it is currently above its mean reversion level, the P/E will tend to fall, suggesting that underweighting stocks would be appropriate.
12. If Nordique’s model is correctly specified, and the market P/E ratio is 22.50 in June 2008, the estimate of the market P/E ratio for August 2008 is closest to:
A. 21.39.
B. 22.04.
C. 22.27.
Answer: B
“Time Series Analysis,” Richard A. DeFusco, CFA, Dennis W. McLeavey, CFA, Jerald E. Pinto, CFA, and David E. Runkle, CFA
2009 Modular Level II, Volume 1, pp. 379-380 Study Session 3-13-d Discuss the structure of an autoregressive model of order p, calculate one- and two-period- ahead forecasts given the estimated coefficients, and explain how autocorrelations of the residuals can be used to test whether the autoregressive model fits the time series.
The one-month forecast is 0.332 + (0.975 × 22.50) = 22.27. The two-month forecast is 0.332 + (0.975 × 22.27) = 22.04.
|

