AIM 1: Calculate, using the one-step and two-step binomial model, the value of a European call or put option.

1、The current price of a non-dividend paying stock is $75. The annual volatility of the stock is 18.25 percent, and the current continuously compounded risk-free interest rate is 5 percent. A 3-year European call option exists that has a strike price of $90. Assuming that the price of the stock will rise or fall by a proportional amount each year, and that the probability that the stock will rise in any one year is 60 percent, what is the value of the European call option?

A) $22.16
 
B) $12.91.
 
C) $7.36. 
 
D) $3.24.

[此贴子已经被作者于2009-6-25 17:02:25编辑过]

The  correct  answer  is C
 
First, we need to calculate the size of an upward movement in the asset’s price as eσ√t = e(0.1825)(1) = 1.20. The size of a downward movement in the stock’s price is 1/1.20 = 0.83.

Next, we project the various paths the stock’s price can follow over the 3 year period. The stock has 4 potential ending values:

Suuu = $75 × 1.2 × 1.2 × 1.2 = $129.60

Suud = Sduu = Sudu = $75 × 1.2 × 1.2 × 0.83 = $89.64

Sudd = Sdud Sddu = $75 × 1.2 × 0.83 × 0.83 = $62.00

Sddd = $75 × 0.83 × 0.83 × 0.83 = $42.89

The only point at which the option finishes in the money is after 3 upward moves, which as a probability of (0.60)(0.60)(0.60) = 0.216.

The value of the option today is therefore ($129.60 - $90) × 0.216 × e(-0.05)(3) = $7.36.

2、A stock that is currently trading at $50 and can either move to $55 or $45 over the next 6-month period. The continuously compounded risk-free rate is 2.25 percent. What is the risk-neutral probability of an up movement?

A) 0.6655.
 
B) 0.6565.
 
C) 0.5656.
 
D) 0.5566.

The  correct  answer  is D

The risk-neutral probability, p, can be calculated as [e(rT)-d] / [u-d].  In this case, r = 0.0225, u = 1.1, d = 0.9, which makes p equal to [e[0.0225*(6/12)] - 0.9] / [1.1 - 0.9] = .5566

3、Calculate the value of a one-year put option today for a stock that currently trades at $40 and can either move to $44 or $36 at the end of a year. The continuously compounded risk-free rate is 3 percent and the put strike price is $40. The put option’s value is closest to:

A) $1.35.
 
B) $2.70.
 
C) $2.02.
 
D) $2.36.

The  correct  answer  is D

One must first calculate the risk-neutral probability measure, π, which is [(e(rT) – d)/(u – d)]. In this case, r = 0.03, u = 1.1, d = 0.9, and T = 1, so π = [(e(0.03) –0.9)/(1.1 – 0.9)] = 0.6523. The value of the put at expiration if the stock price increases is 0, while it is $4 if the stock price decreases. The value of the put, therefore, is e(-0.03)(1 – 0.6523)($4) = $1.35.

4、A stock currently trades at $50. At the end of three months, the stock will either be $55 or $45. The continuously compounded risk-free rate of interest is 5 percent per year. The value of a 3-month European call option with a strike price of $50 is closest to:

A) $2.89.
 
B) $2.55.
 
C) $2.25.
 
D) $2.78. 

The  correct  answer  is D

In this case, u = 1.1, d = 0.9, r = 0.05, and the value of the option is $5 if the stock increases and 0 if the stock decreases. The risk-neutral probability of an up movement, p, can be calculated as:

The value of the call option is, therefore:

5、A stock that currently trades at $40 can either move up or down by 5 percent each year. The continuously compounded risk-free rate is 4 percent. An over-the-counter European call option with 2 years until expiration is set up so that the strike price is determined by the formula $40 + [(years to expiration + 1) × 0.5] in periods when the stock price increases. In periods when the stock price declines, the strike price is $40. What is the value of this 2-year specialized OTC call option?

A) $3.12.
 
B) $3.27.
 
C) $2.56.
 
D) $2.74.

The  correct  answer  is D
The risk neutral probability of an up move is

Cuu = $40 × 1.05 × 1.05 = $44.10

Cud = $40 × 1.05 × 0.95 = $39.90

Cdu = $40 × 0.95 × 1.05 = $39.90

Cdd = $40 × 0.95 × 0.95 = $36.10

Since the strike price is at least $40 in all periods, we know that the option only has value if it follows an up, up path. In period 2, after following an up, up path, the option’s strike price is calculated as $40 + [(0 + 1) ′ 0.5] = $40.50. The intrinsic option value is $44.10 – $40.50 = $3.60.

The value of the option today is

6、A stock is priced at 40 and the periodic risk-free rate of interest is 8 percent. What is the value of a two-period European call option with a strike price of 37 on a share of stock using a binomial model with an up factor of 1.20 and a (risk-neutral) up probability of 67 percent?

A) $20.60.
 
B) $3.57.
 
C) $9.25.
 
D) $9.07. 

The  correct  answer  is D

Two up moves produce a stock price of 40 × 1.44 = 57.60 and a call value at the end of two periods of 20.60. An up and a down move leave the stock price unchanged at 40 and produce a call value of 3. Two down moves result in the option being out of the money. The value of the call option is discounted back one year and then discounted back again to today. The calculations are as follows:

C+ = [20.6(0.67) + 3(0.33)] / 1.08 = 13.6962

C- = [3(0.67) + 0 (0.33)] / 1.08 = 1.8611

Call value today = [13.696(0.67) + 1.8611(0.33)] / 1.08 = 9.07

7、A stock is priced at 38 and the periodic risk-free rate of interest is 6 percent. What is the value of a two-period European put option with a strike price of 35 on a share of stock using a binomial model with an up factor of 1.15 and a risk-neutral probability of 68 percent?

A) $2.58.
 
B) $0.64. 
 
C) $0.57. 
 
D) $2.90. 

The  correct  answer  is C

Given an up probability of 1.15, the down probability is simply the reciprocal of this number 1/1.15=0.87. Two down moves produce a stock price of 38 × 0.872 = 28.73 and a put value at the end of two periods of 6.27. An up and a down move, as well as two up moves leave the put option out of the money. The value of the put option is [0.322 × 6.27] / 1.062 = $0.57.

8、Al Bingly, CFA, is a derivatives specialist who attempts to identify and make short-term gains from trading mispriced options. One of the strategies that Bingly uses is to look for arbitrage opportunities in the market for European options. This strategy involves creating a synthetic call from other instruments at a cost less than the market value of the call itself, and then selling the call. During the course of his research, he observes that Hilland Corporation’s stock is currently priced at $56, while a European-style put option with a strike price of $55 is trading at $0.40 and a European-style call option with the same strike price is trading at $2.50. Both options have 6 months remaining until expiration. The risk-free rate is currently 4 percent.

Bingly often uses the binomial model to estimate the fair price of an option. He then compares his estimated price to the market price. He observes that Dale Corporation’s stock has a current market price of $200, and he predicts that its price will either be $166.67 or $240 in one year. The risk-free rate is currently 4 percent. He also observes that the price of a one-year call with a $220 strike price is $11.11.

Bingly also uses the Black-Scholes-Merton model to price options. His stated rationale for using this model is that he believes the prices of the stocks he analyzes follow a lognormal distribution, and because the model allows for a varying risk-free rate over the life of the option. His plan is to use a statistical technique to estimate the volatility of a stock, enter it into the Black-Scholes-Merton model, and see if the associated price is higher or lower than the observed market price of the options on the stock.

Bingly wishes to apply the Black-Scholes-Merton model to both non-dividend paying and dividend paying stocks. He investigates how the presence of dividends will affect the estimated call and put price.

In the case of the options on Hilland Corporation’s stock, if Bingly were to establish a long protective put position, he could:

A) earn an arbitrage profit of $0.30 per share by selling the call and lending $57.20 at the risk-free rate. 
 
B) earn an arbitrage profit of $0.03 per share by selling the call and borrowing the remaining funds needed for the position at the risk-free rate.
 
C) not earn an arbitrage profit because he should short the protective put position.
 
D) not earn an arbitrage profit because the position is in equilibrium.

The  correct answer is B

Under put-call parity, the value of the call = put + stock – PV(exercise price). Therefore, the equilibrium value of the call = $0.40 + $56 - $55/(1.040.5) = $2.47. Thus, the call is overpriced, and arbitrage is available. If Bingly sells the call for $2.50 and borrows $53.93= $55/(1.040.5), he will have $56.43 > $56.40 (= $56 + $0.40), which is the price he would pay for the protective put position. The arbitrage profit is the difference ($0.03 = $56.43 - $56.40).

The  correct answer is B

The up movement parameter U=1.20, and the down movement parameter D=0.833. We calculate the probability of an up move πU = (1 + 0.04 – 0.833)/(1.2 – 0.833) = 0.564. The call is out of the money in the event of a down movement, and has an intrinsic value of $20 in the event of an up movement. Therefore, the estimated value of the call is C = (0.564) × $20 / (1.04) = $10.85. Thus, the price of $11.11 is too high and the call is overpriced.

The  correct answer is C

The model requires many assumptions, e.g., the distribution of stock prices is lognormal and the risk-free rate is known and constant. Other assumptions are frictionless markets, the options are European, and the volatility is known and constant.

The  correct answer is D

The following are limitations of the BSM:

1、The assumption of a known and constant risk free rate means the BSM is not useful for pricing options on bond prices and interest rates.
2、The assumption of a known and constant asset return volatility makes the BSM not useful in situations where the volatility is not constant which occurs much of the time.
3、The assumption of no taxes and transaction costs makes the BSM less useful.
4、The BSM is designed to price European options and not American options.  

If Bingly forecasts the volatility for a stock and find that it is significantly greater than that implied by the prices of the puts and calls of the stock, he would conclude that:
A) puts and calls are overpriced.
 
B) the puts are overpriced and the calls are underpriced.
 
C) puts and calls are underpriced. 

D) the puts are underpriced and the calls are overpriced.   

The  correct answer is C

There is a positive relationship between the volatility of the stock and the price of both puts and calls. A higher estimate of volatility implies that the prices of both puts and calls should be higher. 

The  correct answer is B

When dividend payments occur during the life of the option, the price of the underlying stock is reduced (on the ex-dividend date). All else being equal, the lower price reduces the value of call options and increases the value of put options.

9、A two-period interest rate tree has the following expected one-period rates:

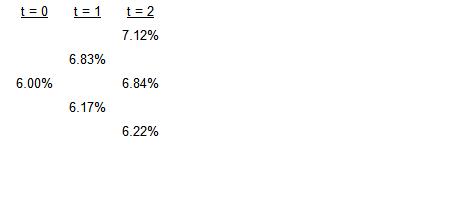
The price of a two-period European interest-rate call option on the one-period rate with a strike rate of 6.25% and a principal amount of $100,000 is closest to:

A) $423.89. 

B) $725.86.

C) $449.33.

D) $704.22. 

The  correct answer is A

1、Calculate the payoffs on the call in percent for I++ and I+? (= I?+):

   I++ value = (0.0712 ? 0.0625) / 1.0712 = 0.00812173.

   I+? value = (0.0684 ? 0.0625) / 1.0684 = 0.00552228.

   Remember that the payoff on the call value is the present value of the interest rate difference based on the raterealized  at     t= 2 because the payment is received at t = 3.

2、Calculate the t = 1 values (the probabilities in an interest rate tree are 50%):

   At t = 1 the values are I+ = [0.5(0.00812173) + 0.5 (0.00552228)] / 1.0683 = 0.00638585.

   At t = 1 the values are I? = [0.5(0) + 0.5 (0.00552228)] / 1.0617 = 0.00260068.

3、Calculate the t = 0 value:

   At t = 0 the option value is [0.5(0.00638585) + 0.5(0.00260068)] / 1.06 = 0.00423893 0.00423893 × 100,000 = $423.89.

10、Which of the following statements concerning the calculation of value at a node in a binomial interest rate tree is most accurate? The value at each node is the:

A) present value of the two possible values from the next period.

B) sum of the present values of the two possible values from the next period.

C) average of the present values of the two possible values from the next period.

D) average of the future values of the two possible values from the next period.

The correct answer is C

The value at any given node in a binomial tree is the present value of the cash flows at the two possible states immediately to the right of the given node, discounted at the 1-period rate at the node under examination.

AIM 2: Calculate, using a two-step binomial model, the value of an American call or put option.

1、The current price of Razor Manufacturing is $20. In each of the next two years you expect the stock price to either move up 20 percent or down 20 percent. The probability of an upward move is 0.65 and the probability of a downward move is 0.35. The risk-free rate is 5 percent. The value of a 2-year American put option with strike price of $24 is closest to:

A) $3.22.
 
B) $3.85.
 
C) $4.00.
 
D) $3.65. 

The correct answer is C

You need to use a two-step binomial model and consider the possibility of early exercise. First calculate the stock price tree. You have S0=20, so the first step results in either SU=20(1.2)=24 or SD=20(0.8)=16 at the end of year one. At the end of the second year the possible outcomes are SUU=24(1.2)=28.80, SUD= SDU=24(0.8)=19.20, or SDD=16(0.8)=12.80. The PV of the expected payoff in the up node is e-0.05[0.00(0.65)+4.80(0.35)]=$1.60. The payoff from early exercise in the up node is max{24-24, 0}=0. Since the PV of the expected payoff exceeds the payoff from early exercise, early exercise in the up node is not optimal. In the down node the PV of the expected payoff is e-0.05[4.80(0.65)+11.20(0.35)]=$6.70. The payoff from early exercise in the down node is max{24-16, 0} = $8.00. So early exercise is optimal in the down node. The value of the option can now be calculated as the PV of the expected payoffs at the end of the first year, or as e-0.05[1.60(0.65)+8.00(0.35)]=$3.65.

If the option is exercised early at the initial node it is worth $4 (=$24 - 20). This value is greater than $3.65, thus, the option should be exercised early at Node 0 and will be worth $4.

2、A stock that is currently trading at $30 can move up or down by 10 percent over a 6-month time period. The probability of the stock moving up in price in a 6-month period is 0.6074. The continuously compounded risk-free rate is 4.25 percent. The value of a 1-year American put option with an exercise price of $32.50 is closest to:

A) $3.42.
 
B) $5.50.
 
C) $2.49.
 
D) $2.75.

The correct answer is D

First calculate the probability of a down move as: pd = 1 – pu = 1 – 0.6074 = 0.3926

Next calculate the terminal values of the option at expiration for each node of the tree:

Suu = $30 × 1.10 × 1.10 = $36.30, Puu = $0

Sud = $30 × 1.10 × 0.90 = $29.70, Pud = $2.80

Sdu = $30 × 0.9 × 1.10 = $29.70, Pdu = $2.80

Sdd = $30 × 0.9 × 0.9 = $24.30, Puu = $8.20

Since this is an American option, we need to compare the discounted present value of the option to its intrinsic value after the end of the first 6-month period to see if the option is worth more dead than alive.

AIM 3: Discuss how the binomial model value converges as time periods are added.

1、As the binomial model of option prices is altered by increasing the number of periods:

A) the results stabilize at 30 periods. 
 
B) it eventually converges to the Black-Scholes-Merton option-pricing model. 
 
C) option values increase. 
 
D) volatility increases. 

The  correct  answer is B

As the option period is divided into more/shorter periods in the binomial option-pricing model, we approach the limiting case of continuous time and the binomial model results converge to those of the continuous-time Black-Scholes-Merton option pricing model.

2、Which of the following statements regarding the Black-Scholes-Merton option-pricing model is TRUE?

A) The Black-Scholes-Merton option-pricing model is the discrete time equivalent of the binomial option-pricing model.
 
B) As the number of periods in the binomial options-pricing model is increased toward infinity, it converges to the Black-Scholes-Merton option-pricing model. 
 
C) The Black-Scholes-Merton model is superior to the binomial option-pricing model in its ability to price options on assets with periodic cash flows. 
 
D) As the periods in the binomial option-pricing model are lengthened, it converges to the Black-Scholes-Merton option-pricing model.

The  correct  answer is B

As the option period is divided into more/shorter periods in the binomial option-pricing model, we approach the limiting case of continuous time and the binomial model results converge to those of the continuous-time Black-Scholes-Merton option pricing model.

3、The pricing results of the Black-Scholes-Merton model can be derived by:

A) lengthening the periods in the binomial model. 
 
B) taking the limit as the periods in the binomial model become shorter. 
 
C) using a regression model of prices on volatility. 
 
D) solving a system of simple mathematical equations.

The  correct  answer is B

As the option period is divided into more/shorter periods in the binomial option-pricing model, we approach the limiting case of continuous time and the binomial model results converge to those of the continuous-time Black-Scholes-Merton option pricing model.

4、Which of the following is a condition needed in order for the binomial tree to approach the Black-Scholes model?

A) Stock prices change in a discrete manner.
 
B) Volatility changes stochastically over the life of the option.
 
C) Interest rates change stochastically over the life of the option.
 
D) The time intervals approach zero.

 The  correct  answer is D

As the length of the time intervals approaches zero, the binomial model converges to the continuous-time Black-Scholes model.