AIM 3: List, define and relate the assumptions underlying the Black-Scholes-Merton model.

1、Which of the following is NOT one of the assumptions of the Black-Scholes-Merton option-pricing model?

A) There are no cash flows over the term of the options. 

B) The volatility is known and remains constant over the term of the option.  

C) The yield curve for risk-free assets is fixed over the term of the option.  

D) There are no taxes and transactions costs are zero for options and arbitrage portfolios. 

The correct answer is C

The yield curve is assumed to be flat so that the risk-free rate of interest is known and constant over the term of the option. Having a fixed yield curve does not necessarily imply that the yield curve is flat.

2、Which of the following is NOT one of the assumptions of the Black-Scholes-Merton (BSM) option-pricing model?

A) Any dividends are paid at a continuously compounded rate.  

B) There are no taxes.  

C) There are no transaction costs.  

D) Options valued are European style. 

The correct answer is A

The BSM model assumes there are no cash flows on the underlying asset.

3、Which of the following is least likely one of the assumptions of the Black-Scholes-Merton option pricing model?

A) The risk-free rate of interest is known and does not change over the term of the option. 

B) There are no cash flows on the underlying asset.  

C) Changes in volatility are known and predictable.  

D) The options are European style.

The correct answer is C

The BSM model assumes that volatility is known and constant. The term predictable would allow for non-constant changes in volatility.

AIM 4: Compute the value of a European option using the Black-Scholes-Merton model on a non-dividend-paying stock.

1、The current price of a stock is $55. A put option with a $50 strike price that expires in 3 months is available. If N(d1) = 0.8133, N(d2) = 0.7779, the underlying stock exhibits an annual standard deviation of 25 percent, and current risk free rates are 3.25 percent, the Black-Scholes value of the put is closest to:

A) $1.25. 

B) $1.50. 

C) $0.75. 

D) $5.00.

The correct answer is C

This question is not as straight-forward as it looks because N(d1) and N(d2) are given instead of N(-d1) and N(-d2) which are needed to solve for the price of a put.

N(-d1) = 1 – 0.8133 = 0.1867; N(-d2) = 1 – 0.7779 = 0.2221

The Black-Scholes formula for pricing a put is P= Xe(-rT) N(-d2) – SoN(-d1)

P= ($50e(-0.0325*0.25) * 0.2221) - ($55 * 0.1867) = $0.75

2、Using the Black-Scholes model, compute the value of a European call option using the following imputs:

Underlying stock price: $100

Exercise price: $90

Risk-free interest rate: 5%

Volatility: 20%

Dividend yield: 0%

Time to expiration: one year

The Black-Scholes call option price is closest to:

A) $13.65. 

B) $16.71. 

C) $15.33. 

D) $17.99.

The correct answer is B

This value is obtained using the Black-Scholes model for call option without dividends:

So d1=(ln(100/90)+(0.05+0.202/2))/0.2√1=0.8768 and using the table, N(0.88)=0.8106. d2=0.8768-0.2√1=0.6768, so from the table,N(d2)=N(0.68)=0.7517.

So the call value is 100(0.8106)-90e(-0.05)(0.7517)=$16.71.

3、Using the Black-Scholes model compute the value of a European put option using the following inputs:

Underlying stock price: $90

Exercise price: $90

Risk-free interest rate: 5%

Volatility: 20%

Dividend yield: 0%

Time to expiration: one year

The Black-Scholes put option price is closest to:

A) $4.11. 

B) $5.89. 

C) $6.12.

D) $5.01.

The correct answer is D

It is found as follows:

Put Price = Xe-.rt * [1 - N(d2)] – S * [1 - N(d1)]

Where d1=(ln(90/90)+(.05+.04/2)1)/.2√1)=.35 and using the Normal Z table, 1-N(.35)=1-.6368=.3632.

d2=.35-.2√1=.15, and using the Normal Z table, 1-N(.15)=1-.5596=.4404.

So the put value = 90e(-.05*1)(.4404) - 90(.3632)=$5.01

4、Consider a 120-day call option at 28 on a stock selling at 30 with an annualized standard deviation of 0.20 when the continuously compounded risk-free rate is 7 percent. The value of the call is closest to: [round d1 and d2 rather than interpolate for N(.)]

CT = [ST x N(d1)] - [Xe-rTN(d2)]

where:

d1 = ln(ST / X) + [r + σ2/2]T / σ √T

d2 = d1 - σ √T

Figure 1: Cumulative Standard Normal Probability

0.03

0.04

0.05

0.06

0.6	0.7357	0.7389	0.7422	0.7454
0.7	0.7673	0.7704	0.7734	0.7764
0.8	0.7967	0.7995	0.8023	0.8051

A) $3.02.  

B) $3.12.  

C) $3.33. 

D) $3.07. 

The correct answer is D

T=120/365 = 0.328767
d₁ =0.8596 ≈ 0.86 N(d₁) = 0.8051
d₂ =0.7449 ≈ 0.74 N(d₂) = 0.7704
c = $3.07

5、 Consider a 145-day put option at 30 on a stock selling at 27 with an annualized standard deviation of 0.30 when the continuously compounded risk-free rate is 4 percent. The value of the put option is closest to: [round d1 and d2 rather than interpolate for N(.)].

P_T = [Xe^{-r (T)} × (1 - N(d₂))] - [S_T × (1 - N(d₁))]
where:
d₁ = [ln(S_t / X) + [r + σ²/2](T) ] / σ √(T-t)
d₂ = d₁ - σ √(T)

A) $3.64. 

B) $3.32.  

C) $3.97. 

D) $4.07.

The correct answer is A

T=145/365 = 0.39726

d₁ = [ln(27/30) + [.04 + .3²/2](.39726)] / (.3√.39726)

    = (-.10536052 + .0337671) / .18908569

    = -.07159342 / .18908569

    = -0.37863
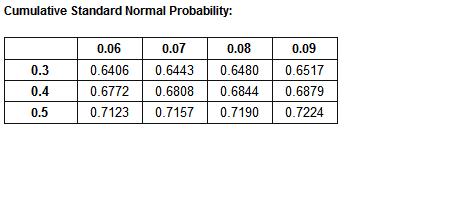
d₁ = -0.37863 ≈ -0.38 N(d₁) = 1 -0.6480 = 0.3520

d₂ = -0.37863 - .3√.39726

    = -0.37863 - .18908569

    = -.56771569

    = -.56772
d₂ = -0.56772 ≈ -0.57 N(d₂) = 1 - 0.7157 = 0.2843

P_T = 30e^-.04(.39726) (1-.2843) – 27(1-.352)

    = (29.527056 × .7157) – 17.496

    = 21.1325 – 17.496
p = $3.64

AIM 6: Compute the value of a European option using the Black-Scholes-Merton model on a dividend-paying stock.

1、Dividends on a stock can be incorporated into the valuation model of an option on the stock by:

A) subtracting the present value of the dividend from the current stock price. 

B) subtracting the future value of the dividend from the current stock price.  

C) adding the future value of the dividend to the option value. 

D) adding the present value of the dividend to the current stock price. 

The correct answer is A

The option pricing formulas can be adjusted for dividends by subtracting the present value of the expected dividend(s) from the current asset price.

2、Compared to the value of a call option on a stock with no dividends, a call option on an identical stock expected to pay a dividend during the term of the option will have a:

A) lower value only if it is an American style option.  

B) lower value in all cases.  

C) higher value in all cases. 

D) higher value only if it is an American style option.

The correct answer is B

An expected dividend during the term of an option will decrease the value of a call option.

3、The value of a put option will be higher if, all else equal, the:

A) underlying asset has less volatility.  

B) exercise price is lower.  

C) underlying asset has positive cash flows.  

D) stock price is higher.

The correct answer is C

Positive cash flows in the form of dividends will lower the price of the stock making it closer to being "in the money" which increases the value of the option as the stock price gets closer to the strike price.

AIM 7: List and discuss the various methods that estimate future volatility.

1、The implied volatility of interest rates can be best computed using the market price of an:

A) interest rate forward contract. 

B) interest rate futures contract. 

C) interest rate call option contract. 

D) S& 500 option contract.

The correct answer is D

Implied volatility of interest rates can be best computed using interest rate option contracts. Forward or futures contract pricing models do not have interest rate volatility as an input. S& 500 option contracts have the volatility of the S& 500 index (and not interest rates) as an input.

2、Which of the following methods is NOT used for estimating volatility inputs for the Black-Scholes model?

A) Using long term historical data. 

B) Using the most current historical data. 

C) Using exponentially weighted historical data. 

D) Models of changing volatility.

The correct answer is D

The volatility is constant in the Black-Scholes model.

3、If we use four of the inputs into the Black-Scholes-Merton option-pricing model and solve for the asset price volatility that will make the model price equal to the market price of the option, we have found the:

A) implied volatility.  

B) historical volatility.  

C) market volatility.  

D) option volatility.

The correct answer is A

The question describes the process for finding the expected volatility implied by the market price of the option.

4、Which of the following is TRUE for an option's price? An option's price is:

A) a decreasing function of the underlying asset's volatility. 

B) unaffected by changes in the underlying asset's volatility. 

C) an increasing function of the underlying asset's volatility. 

D) a decreasing function of the underlying asset's volatility when it has a long time remaining until expiration and an increasing function of its volatility if the option is close to expiration.

The correct answer is C

Since an option has limited risk but significant upside potential, its value always increases when the volatility of the underlying asset increases.