

AIM 3: Define and interpret the forward rate, and compute the forward rate given series of spot rates or forward rates.
1、 Use the following Treasury bond prices to answer the next four questions. Assume the prices are for settlement on June 1, 2005, today’s date. Assume semiannual coupon payments:
|
Coupon |
Maturity |
Price |
|
7.500% |
12/1/2005 |
102-9 |
|
12.375% |
6/1/2006 |
107-15 |
|
6.750% |
12/1/2006 |
104-15 |
|
5.000% |
6/1/2007 |
102-9+ |
The discount factors associated with the bonds maturing in December 2005 and June 2006, are closest to:
A) 0.9696/0.9858.
B) 0.9858/0.9546.
C) 0.9546/0.9696.
D) 0.9778/0.9696.
The correct answer is B
We must calculate the 6-month discount factor first. This is done by dividing today’s price by the final payment’s par + coupon: 
The spot rates associated with the discount factors determined in the previous question are closest to:
A) 2.25%/4.87%.
B) 1.82%/7.56%.
C) 3.26%/5.87%.
D) 2.88%/4.70%.
The correct answer is D

Given the spot rates for the 6-month and 1-year maturing bond, the 6-month forward rate 6 months from now is closest to:
A) 5.86%.
B) 6.04%.
C) 6.54%.
D) 7.28%.
The correct answer is C

The correct answer is C
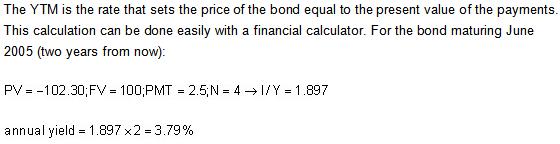
2、Use the Treasury bond prices given below for the following four problems. Assume the prices are for settlement on June 1, 2005, today’s date. Assume semiannual coupon payments:
|
Coupon |
Maturity |
Price |
|
6.00% |
12/1/2005 |
99–15 |
|
7.00% |
6/1/2006 |
98–27+ |
|
8.00% |
12/1/2006 |
101–29 |
|
9.00% |
6/1/2007 |
102–9 |
The discount factors associated with the bonds maturing in December 2005 and June 2006, respectively, are closest to:
A) 0.9587; 0.9157.
B) 0.9458; 0.9013.
C) 0.9319; 0.8769.
D) 0.9657; 0.9225.
The correct answer is D
We must calculate the discount factor for the December bond first. This is done by dividing today’s price by the final payment’s par + coupon:
(99 + 15/32)/(100 + 6/2) = 0.9657. The 12-month discount factor d2 solves the following equation: [(7/2)(0.9657)]+[(100+7/2)(d2)] = 98+(27.5/32); d2=0.9225.
The spot rates associated with the discount factors of the previous problem are closest to:
A) 4.87%; 6.23%.
B) 5.48%; 6.78%.
C) 7.10%; 8.23%.
D) 6.26%; 7.05%.
The correct answer is C
The easiest way to do this given the discount factors is to use the formula
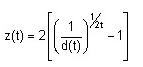
where z(t) is the spot rate associated with the discount factors d(t). The first spot rate, which pertains to the bond maturing in December 2003, is equal to (1/0.9657 – 1) × 2 = 7.10%. The second spot rate, which pertains to the payment being made in June 2004, is equal to ((1/0.9225)0.5 – 1) × 2 = 8.23%.
Given the spot rates for the 6-month and 1-year maturing bond, the forward rate inherent in those figures is closest to:
A) 9.37%.
B) 4.68%.
C) 5.74%.
D) 6.96%.
The correct answer is A
The key to calculating forward rates is to understand that the longer spot rate has to be equivalent to the product of the two shorter rates. In this case, an investment in a 1-year rate held over the year has to generate the same cash flow as investing for the first six months and then reinvesting in another 6-month bond. Therefore, the forward rate implied by the annual and the 6-month spot rate is equal to:
[attach]13889[/attach]
= 4.6831%
4.6831 x 2 = 9.37% annualized return



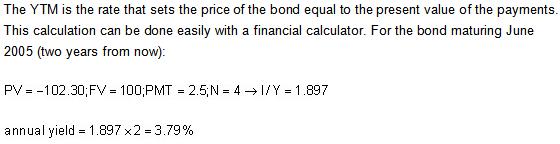
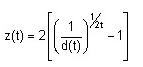

3、Which of the following statements concerning a forward rate is FALSE? A forward rate is:
A) the market’s best guess as to an interest rate that will exist in the future.
B) an interest rate that can be locked in for some future time period.
C) the interest rate that makes an investor indifferent to investing over a long time period or investing over two or more shorter time periods.
D) the rate of interest an investor would earn from now until some point in the future.
The correct answer is D
The rate of interest an investor could invest at today until some point in the future is the spot rate. The other three statements correctly identify the three possible interpretations of a forward rate. A forward rate can be interpreted as a break even rate, a locked-in rate for some future period, or an expectation of future spot interest rates.
4、If the one-year spot rate is 7 percent and the one-year forward rate is 7.4 percent, what is the two-year spot rate?
A) 7.12 %.
B) 7.27%.
C) 7.40%.
D) 7.20%.
The correct answer is D
The two-year spot rate: ((1+0.07)(1+0.074)).5 - 1 = 0.072, or 7.2 percent.
5、Assume the one-year spot rate is 4 percent, the two-year spot rate is 4.5 percent, and the three-year spot rate is 5 percent. Which of the following statements is TRUE?
A) The one-year rate that will exist one year from today is 5.5 percent.
B) The one-year rate that will exist two years from today is 5 percent.
C) The two-year rate that will exist one year from today is 5.5 percent.
D) The rate that an investor can earn on a sum invested today for the next three years is 5.5 percent.
The correct answer is C
It might be best to draw a set of timelines for this problem.
The one-year rate that will exist one year from today is:
(1.045)2/(1.04) ? 1 = 0.05, or 5%.
The one-year rate that will exist two years from today is:
(1.05)3/(1.045)2 ? 1 = 0.06, or 6%.
The two-year rate that will exist one year from today is:
(1.05)3/(1.04)) = (1.113)0.5 = 1.055 ? 1 = 0.055, or 5.5%.
Note that the rate that an investor could earn on a sum invested today for the next three years would be equal to the three-year spot rate of 5%.
6、If the five-year spot rate is 6.1 percent and the four-year spot rate is 5.9 percent, what is the only rate that can be computed?
A) The four-year forward rate starting one year from today is 6.9%.
B) The one-year forward rate starting four years from today is 6.9%.
C) The one-year forward rate starting four years from today is 7.4%.
D) The four-year forward rate starting one year from today is 7.4%.
The correct answer is B
Using the current five-year spot rate and the current four-year spot rate, we can derive the one-year forward rate starting four years from today. The formula is: (1.061)5/(1.059)4 = (1+R)1 – 1 = 0.069, or 6.9 percent.
7、Use this table for the following questions.
|
Maturity (Years) |
STRIPS Price |
Spot Rate |
Forward Rate |
|
0.5 |
98.7654 |
2.50% |
2.50% |
|
1.0 |
97.0662 |
3.00% |
3.50% |
|
1.5 |
95.2652 |
3.26% |
3.78% |
|
2.0 |
93.2775 |
????% |
????% |
The 6-month forward rate in 1.5 years (ending in year 2.0) is closest to:
A) 4.26%.
B) 4.57%.
C) 4.11%.
D) 4.04%.
The correct answer is A
First, calculate the spot rate in year 2.
2 * [(100/93.2775)^(1/4) - 1] = 3.51%
Next, calculate the forward rate in year 2.
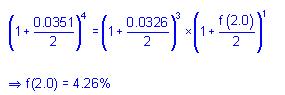
The value of a 1.5-year, 6 percent semiannual coupon, $100 par value bond is closest to:
A) $102.19.
B) $103.42.
C) $104.00.
D) $105.66.
The correct answer is C
[此贴子已经被作者于2009-6-26 15:54:24编辑过]
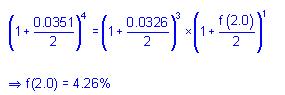

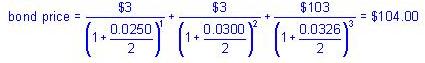
8、The Treasury spot rate yield curve is closest to which of the following curves?
A) Zero-coupon bond yield curve.
B) Par bond yield curve.
C) Reinvestment rate yield curve.
D) Forward yield curve rate.
The correct answer is A
The spot rate yield curve shows the appropriate rates for discounting single cash flows occuring at different times in the future. Conceptually, these rates are equivalent to yields on zero-coupon bonds. The par bond yield curve shows the YTMs on coupon bonds by maturity. Forward rates are expected future short-term rates. Reinvestment rates are not part of the spot rate yield curve.
9、
|
Maturity (Years) |
STRIP Price |
Spot Rate |
Forward Rate |
|
0.5 |
98.7654 |
2.50% |
2.50% |
|
1.0 |
97.0662 |
3.00% |
3.50% |
|
1.5 |
95.2652 |
3.26% |
3.78% |
|
2.0 |
93.2775 |
?.??% |
?.??% |
The 2-year spot rate is closest to:
A) 3.42%.
B) 3.87%.
C) 4.02%.
D) 3.51%.
The correct answer is D
N = 4; PV = ?93.2775; PMT = 0; FV = 100; CPT → I/Y = 1.755%;
z(0.5) = 1.755% × 2 = 3.51%.
| 欢迎光临 CFA论坛 (http://forum.theanalystspace.com/) | Powered by Discuz! 7.2 |