AIM 1: Define and compute the dollar value of a basis point (DV01) of a fixed income security, and interpret DV01 of a fixed income security, given a change in yield and the resulting change in price.

1、The price value of a basis point for a 7% coupon, semiannual pay, 10-year bond with a $1,000 par value, currently trading at par, is closest to:

A) $0.71.
 
B) $1.42.
 
C) $67.10.
 
D) $33.55.

The correct answer is A 

The price value of a basis point is the price given a 1 basis point change in the discount rate.
N = 20; PMT = 35; FV = 1,000; I/Y = 7.01/2 = 3.505; CPT → PV = 999.29
$1,000 – $999.29 = $0.71.

2、The price value of a basis point (PVBP) for a 7-year, 10 percent semiannual pay bond with a par value of $1,000 and yield of 6 percent is closest to:

A) $0.28.
 
B) $0.92.
 
C) $0.00.
 
D) $0.64.

The correct answer is D

PVBP = initial price – price if yield changed by 1 bps.

Initial price:                                 Price with change:
 
FV = 1000                                   FV = 1000
 
PMT = 50                                    PMT = 50
 
N = 14                                        N = 14
 
I/Y = 3%                                     I/Y = 3.005
 
CPT PV = 1225.92                  CPT PV = 1225.28
 

PVBP = 1,225.92 – 1,225.28 = 0.64
PVBP is always the absolute value.

3、The price value of a basis point (PVBP) for a 18 year, 8 percent annual pay bond with a par value of $1,000 and yield of 9 percent is closest to:

A) $0.44.
 
B) $0.82.
 
C) $0.63.
 
D) $0.80.
 

The correct answer is B

PVBP = initial price – price if yield changed by 1 bps.

Initial price:                                  Price with change:
 
FV = 1000                                    FV = 1000
 
PMT = 80                                     PMT = 80
 
N = 18                                          N = 18
 
I/Y = 9%                                       I/Y = 9.01
 
CPT PV = 912.44375               CPT PV = 911.6271
 

PVBP = 912.44375 – 911.6271 = 0.82
PVBP is always the absolute value.

4、The price value of a basis point (PVBP) of a bond is $0.75. If the yield on the bond goes up by 1 bps, the price of the bond will:

A) increase by $0.75.
 
B) increase or decrease by $0.75.
 
C) decline by $0.75.
 
D) is less volatile than a bond with a PBVP of $0.50.

The correct answer is C

Inverse relationships exist between price and yields on bonds. The larger the PVBP, the more volatile the bond’s price.

5、For a given bond and yield, the dollar value of a one basis point change in yield is typically:

A) greater for a yield increase.
 
B) equal for a yield increase and decrease.
 
C) unrelated to the bonds convexity.
 
D) greater for a yield decrease.

The correct answer is D

When you calculate the dollar value of a basis point for a 1bp uptick and 1 bp downtick, it is greater for a yield decrease. This is a function of bond convexity.

6、For a 20-year, $1,000 par value, 6 percent coupon T-bond yielding 5 percent, the dollar value of a basis point (DV01) and associated percentage price change (PPC) are closest to:

A) $1.37 and 0.12%.
 
B) $0.14 and 0.01%.
 
C) $0.57 and 0.06%.
 
D) $2.45 and 0.20%.

The correct answer is A

N=20×2; I/Y=5/2; PMT=60/2; FV=1000; CPT→PV=1,125.51=V0
N=20×2; I/Y=4.99/2; PMT=60/2; FV=1000; CPT→PV=1,126.88=V-
DV01=1,126.88-1,125.51=$1.37. PPC=DV01/V0=1.37/1,125.51=0.0012.

7、June Klein, CFA, manages a $200 million (market value) U.S. government bond portfolio for a large institution. Klein anticipates a small, parallel shift in the yield curve of 10 basis points and wants to fully hedge the portfolio against any such change. Klein would like to use the T-bond futures contract to implement the hedge. She tabulates some essential information about her portfolio and the corresponding futures contract. The results are shown in Table 1.

Table 1: Portfolio and Treasury Bond Futures Contract Characteristics

Klein is not as comfortable with the T-bond futures contract as she would like to be. Consequently, she decides to familiarize herself with the characteristics of the futures contract and its associated delivery process. She collects all of the deliverable bonds for the futures contract. This information is shown in Table 2. Klein will test her understanding using the highlighted bond in Table 2. The price value of a basis point (PVBP) are per $1 million par value.

Table 2: Treasury Bonds Deliverable for T-Bond Futures Contract

Klein's broker supplies the characteristics of the Treasury bond that is currently the cheapest-to-deliver bond. These are shown in Table 3.

Table 3: Cheapest-to-Deliver Treasury Bond

Klein wants to compute the interest rate sensitivity of the highlighted bond in Table 2. She assumes that the yield increases by one basis point. How much, per $1 million par position, will the value of this bond change (to the nearest dollar)?

A) -$1,211.

B) -$12.

C) $121,123.

D) -$121,123.

The correct answer is A

This is the price value of a basis point (PVBP) per one million dollar par as shown in Table 2.

The correct answer is D

PVBP = (0.0001) × D × (price + accrued interest) × 10,000
Note: The 10,000 is to convert the price to $1,000,000 par to match the PVBP units.
Rearranging, D = PVBP ÷ (price + interest) = 1,211.2284 ÷ (133.75 + 2.5824) = 8.88

The correct answer is B

Change in portfolio value = -0.001 × duration × portfolio value. Change in portfolio value = -0.001 × 8.88438 × $100,000,000 = ?$888,438.

AIM 4: Define and compute effective duration, and interpret the effective duration of a fixed income security, given a change in yield and the resulting change in price.

1、The most commonly used measure of interest-rate risk is:

A) duration.  

B) maturity. 

C) yield.  

D) coupon.

The correct answer is A

Duration measures the sensitivity of an instrument’s market value to changes in interest rates. Note that maturity, yield, and coupon, are all features of bonds that tie into determining duration.

2、A 10-year, 11 percent annual coupon bond with $100 par value currently yields 9 percent. What is the duration of the bond given a 50 basis point change in yield?

A) 4.80 years.  

B) 6.95 years. 

C) 6.19 years.  

D) 7.27 years.

The correct answer is C

I/Y = 9.00; FV = 100; N = 10; PMT = 0.11 x 100 = 11; PV = V0 = 112.84

I/Y = 8.50; FV = 100; N = 10; PMT = 0.11 x 100 = 11; PV = V- = 116.40

I/Y = 9.50; FV = 100; N = 10; PMT = 0.11 x 100 = 11; PV = V+ = 109.42

D = effective duration     =  [(V- - V+) / (2V0(Δy))]

                                   = (116.40 – 109.42)/(2x112.84x0.005)

                                   = 6.19

3、A major problem with the use of duration in interest rate risk management is that it assumes:

A) differential sensitivity of assets and liabilities to changes in interest rates.  

B) a nonlinear relationship between prices and rates.

C) only a single change in interest rates over the planning horizon.  

D) an inverse relationship between prices and rates.

The correct answer is C

Duration assumes only a single and parallel shift in interest rates over the interest rate management planning horizon.

4、A 10-year maturity Treasury bond has a par value of $10,000 and a 5 percent coupon. The yield on the bond is 4.5 percent. Assume that the yield can fall to 4.45 percent or rise to 4.55 percent.

The effective duration for the bond is closest to:

A) 8.07.  

B) 7.86. 

C) 7.24.  

D) 7.61.

The correct answer is B

N = 20; I/Y = 4.45/2; PMT = 500/2; FV = 10,000; CPT PV = 10,440.05 = V–

N = 20; I/Y = 4.55/2; PMT = 500/2; FV = 10,000; CPT PV = 10,358.33 = V+

N = 20; I/Y = 4.50/2; PMT = 500/2; FV = 10,000; CPT PV = 10,399.09 = V0

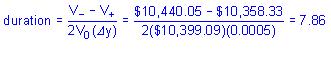
The effective convexity of the bond is closest to:

A) 57.69.  

B) 76.93.   

C) 38.46.

D) 19.23.

The correct answer is B

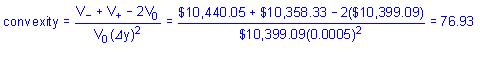
Given your answers to the two prior questions, the percentage price change associated with a 20-basis-point increase in yield is closest to a:

A) decrease of 1.56%.   

B) decrease of 1.60%.  

C) decrease of 1.58%.   

D) decrease of 1.54%. 

The correct answer is A

percentage price change = [–duration ′ Dy ′  [(1/2)+100]  ′ convexity ′ Dy2 ′ 100]

-7.86(0.002)100 + (0.5)76.93(0.002)²(100) = -1.5566

5、A 12-year, 5 percent semiannual coupon bond with $100 par value currently yields 8.00 percent. What is the duration of the bond given a 100 basis point increase and decrease in yield?

A) 7.80.  

B) 12.56. 

C) 16.78.  

D) 8.38.

The correct answer is D

I/Y = 8/2=4; FV = 100; N = 24; PMT = 0.05/2 x 100 = 2.50; PV = V0 = 77.13

I/Y = 7/2=3.50; FV = 100; N = 24; PMT = 0.05/2 x 100 = 2.50; PV = V- = 83.94

I/Y = 9/2=4.50; FV = 100; N = 24; PMT = 0.05/2 x 100 = 2.50; PV = V+ = 71.01

D = effective duration = (V- - V+)/2V0(Δy)

= (83.94-71)/(2x77.13x0.01)

= 8.38 years

6、Which of the following statements regarding duration is FALSE?

A) Duration is unitless.  

B) Duration is a measure of percentage change in price for a given change in yield.

C) Duration of a portfolio of bonds is equal to the market value weighted average of the duration of individual bonds in the portfolio.

D) Other things equal, bonds with longer durations tend to have higher yields.

The correct answer is A

Duration is a measure of percentage change in price for a given change in yield. Hence it is not unitless like beta. Since duration is a measure of risk for bonds, bonds with higher duration tend to have a higher yield (other things being equal). Portfolio duration can be computed as simply market-value weighted durations of individual bonds in the portfolio.

7、A 12-year, 8 percent annual coupon bond with $100 par value currently sells at par. The bond is callable at 102. What is the effective duration of the bond assuming interest rates change by 100 basis points?

A) 5.85.  

B) 4.58. 

C) 7.55.  

D) 10.50.

The correct answer is B

Since the bond is selling at par, its yield = coupon rate = 8%.

V0 = Par = 100.

I/Y = 7.00; FV = 100; N = 12; PMT = 0.08 x 100 = 8; PV = V- = 107.94.

Since the call price is 102 which is lower than 107.94, we use V- = 102

I/Y = 9.00; FV = 100; N = 12; PMT = 0.08 x 100 = 8; PV = V+ = 92.84     

D = Duration = (V- - V+)/2V0(Δy)         

                     = (102-92.84)/(200x0.01)

                     = 4.58

8、Duration of a bond can be defined as the:

A) sensitivity of the value of the bond to a change in maturity.  

B) sensitivity of the value of the bond to a change in interest rates. 

C) weighted-average maturity of a bond portfolio.  

D) sensitivity of the value of the bond to a change in the value of market portfolio.

The correct answer is B

Duration is the first derivative of price with respect to yield and hence measures the sensitivity of the value of the bond to a change in interest rates. Weighted average maturity does not take into account cash flows or yield. Sensitivity of the value of an asset to change in maturity is not defined; and sensitivity of the value of an asset to change in the value of the market portfolio is defined as beta.

9、Vijay Ranjin, CFA, is a portfolio manager with Golson Investment Group. He manages a fixed-coupon bond portfolio with a face value of $120.75 million and a current market value of $116.46 million. Golson’s economics department has forecast that interest rates are going to change by 50 basis points. Based on this forecast, Ranjin estimates that the portfolio’s value will increase by $2.12 million if interest rates fall and will decrease by $2.07 million if interest rates rise. Which of the following choices is closest to the portfolio’s effective duration?

A) 0.4

B) 3.6

C) 2.9

D) 4.3

The correct answer is B

Effective duration = (price when interest rates fall ? price when interest rates rise) / (2 × initial price × basis point change)

= (118.58 – 114.39) / (2 × 116.46 × 0.005) = 3.60.

10、Which of the following statements about duration is FALSE?

A) Effective duration is the exact change in price due to a 100 basis point change in rates.

B) The numerator of the effective duration formula assumes that market rates increase and decrease by the same number of basis points.

C) Price volatility has a direct relationship with interest rate risk.

D) For a specific bond, the effective duration formula results in a value of 8.80%. For a 50 basis point change in yield, the approximate change in price of the bond would be 4.40%.

The correct answer is A

Effective duration is an approximation because the duration calculation ignores the curvature in the price/yield graph.

11、A bond with an 8% semi-annual coupon and 10-year maturity is currently priced at $904.52 to yield 9.5%. If the yield declines to 9%, the bond’s price will increase to $934.96, and if the yield increases to 10%, the bond’s price will decrease to $875.38. Estimate the percentage price change for a 100 basis point change in rates.

A) 4.35%.

B) 2.13%.

C) 8.41%.  

D) 6.58%.

The correct answer is D

The formula for the percentage price change is: (price when yields fall – price when yields rise) / 2 × (initial price) × 0.005 = ($934.96 – 875.38) / 2($904.52)(0.005) = $59.58 / $9.05 = 6.58%. Note that this formula is also referred to as the bond’s effective duration.

12、When calculating duration, which of the following bonds would an investor least likely use effective duration on rather than modified duration?

A) Option-free bond.

B) Callable bond.

C) Putable bond.

D) Convertible bond.

The correct answer is A

The duration computation remains the same. The only difference between modified and effective duration is that effective duration is used for bonds with embedded options. Modified duration assumes that all the cash flows on the bond will not change, while effective duration considers expected cash flow changes that may occur with embedded options.

13、The goal of computing effective duration is to get a:

A) more accurate measure of the bond's price sensitivity when embedded options exist.

B) preliminary estimate of modified duration.

C) preliminary estimate of Macaulay duration.

D) measure of duration that is effectively constant for the life of the bond.

The correct answer is A

The point of effective duration is to consider expected changes in cash flow from features such as embedded options. When embedded options exist, the effective duration will give a better measure of the bond’s price sensitivity to interest rate changes.

14、When compared to modified duration, effective duration:

A) factors in how embedded options will change expected cash flows.

B) places less weight on recent changes in the bond's ratings.

C) places more weight on recent changes in the bond's ratings.

D) is equal to modified duration for callable bonds but not putable bonds.

The correct answer is A

The point of effective duration is to consider expected changes in cash flow from features such as embedded options.

AIM 5: Define and compute convexity, and interpret the convexity of a fixed income security, given a change in yield and the resulting change in price.

1、If a 12-year, 8 percent annual coupon bond with $100 par value is currently selling at par what is the convexity of the bond?

A) 57.0. 

B) 98.0. 

C) 100.5. 

D) 78.0.

The correct answer is D

Since the bond is selling at par, it’s yield = coupon rate = 8%.

V0 = Par = 100.

For convexity, change in yield used in calculations is arbitrary – so we use 100 bps in our calculations below.

I/Y = 7.00; FV = 100; N = 12; PMT = 0.08 x 100 = 8; PV = V- = 107.94

I/Y = 9.00; FV = 100; N = 12; PMT = 0.08 x 100 = 8; PV = V+ = 92.84

convexity = (107.94+92.84-200)/(100x0.012)= 78

2、Which of the following statements describe a property of bond convexity? Convexity:

  I.  increases as yields increase.

 II.  increases with the square of maturity.

III.  measures the rate of change in duration.

IV.  increases if the coupon on a bond is increased.

A) II and III only.   

B) I and III only.

C) II and IV only. 

D) III and IV only.

The correct answer is A

Convexity is inversely related to yield and is indirectly related to the coupon rate on a bond. Convexity is the second derivative of price with respect to yield, which means that convexity measures the rate of change in duration. Convexity increases with the square of maturity.

3、Why is convexity a good thing for a bond holder? Because when compared to a low convexity bonds a high convexity bond:

A) is usually underpriced. 

B) has better price changes regardless of the direction of the yield change. 

C) is more sensitive to interest rate changes, increasing the potential payoff. 

D) has improved estimation of price changes.

The correct answer is B

Relative to a bonds with low convexity, the price of a bond with high convexity will increase more when rates decline and decrease less when rates rise.

4、How does the convexity of a bond influence the yield on the bond? All else the same, for a bond with high convexity investors will require:

A) a lower yield. 

B) a higher yield. 

C) the same yield as for a low convexity bond. 

D) a higher or lower yield depending on the bond's duration.

The correct answer is A

Convexity is to the advantage of the bond holder because a high-convexity bond's price will decrease less when rates increase and will increase more when rates decrease than a low-convexity bond's price.

5、With respect to an option-free bond, when interest-rate changes are large, the duration measure will overestimate the:

A) associated change in the bond's rating.

B) final bond price from a given increase in interest rates.

C) fall in a bond's price from a given increase in interest rates.

D) increase in a bond's price from a given increase in interest rates.

The correct answer is C

When interest rates increase by 50-100 basis points or more, the duration measure overestimates the decrease in the bond’s price.

6、For a given change in yields, the difference between the actual change in a bond’s price and that predicted using the duration measure will be greater for:

A) a bond with greater convexity.

B) a short-term bond.

C) inverse convexity.

D) a bond with less convexity.

The correct answer is A

Duration is a linear measure of the relationship between a bond’s price and yield. The true relationship is not linear as measured by the convexity. When convexity is higher, duration will be less accurate in predicting a bond’s price for a given change in interest rates. Short-term bonds generally have low convexity.

7、Convexity is more important when rates are:

A) unstable.

B) high.

C) low.

D) depends on whether the note is selling at a premium or a discount.

The correct answer is A

Since interest rates and the price of bonds are inversely related, unstable interest rates will lead to larger price fluctuations in bonds. The larger the change in the price of a bond the more error will be introduced in determining the new price of the bond if only duration is used because duration assumes the price yield relationship is linear when in fact it is a curved convex line. If duration alone is used to price the bond, the curvature of the line magnifies the error introduced by yield changes, and makes the convexity adjustment even more important.

AIM 6: Estimate, given the DV01, the duration and the convexity of a fixed income security, the price change of a security.

1、A 12-year, 8 percent semiannual coupon bond with $100 par value currently trades at $78.75 and has an effective duration of 9.8 years and a convexity of 130.0. What is the price of the bond if the yield falls by 150 basis points?

A) $91.48. 

B) $67.17. 

C) $86.47. 

D) $95.43.

The correct answer is A

Percentage price change = [(-) (effective duration)( Δy)]+[(1/2)(convexity)( Δy)2]

= [(-)(9.80)(-0.015)]+[(0.5)(130)(-0.015)2] = 16.16

Estimated price = 78.75(1+0.1616) = $91.48

2、Estimated price changes using only duration tend to:

A) overestimate the increase in price that occurs with a decrease in yield for large changes in yield.

B) underestimate the decrease in price that occurs with an increase in yield for large changes in yield.

C) underestimate the increase in price that occurs with a decrease in yield for large changes in yield. 

D) overestimate the increase in price that occurs with a decrease in yield for small changes in yield.

The correct answer is C

For large changes in yield, duration underestimates the increase in price that occurs with a decrease in yield, and overestimates the decrease in price that occurs with an increase in yield. For small changes in yield, the estimated price change and actual price change are very close to the same.

3、A bond has an effective duration of 7.5 and a convexity of 104.0. If yields rise by 82 bps, the price of the bond will:

A) increase by 6.50%.

B) decrease by 5.80%.   

C) increase by 6.15%. 

D) decrease by 6.15%.   

The correct answer is B

%DPrice = [–7.5 ′ 0.0082 ′ 100] ? [(1/2) ′ 104 ′ 0.00822 ′ 100] = –5.80%.

4、A 12-year, 6 percent, option-free bond is currently trading at par. The bond has a duration of 8.38 years and a convexity of 91.93. Your estimate of the percent price change (PPC) associated with a 100 basis point decrease in yield is closest to:

A) 7.92 percent increase.  

B) 8.84 percent decrease. 

C) 7.92 percent decrease.  

D) 8.84 percent increase.

The correct answer is D

ΔV-% ≈ [-duration×(Δy)×100]+[0.5×convexity×(Δy)2×100]=[-8.38×(-0.01) ×(100)]+[0.5×(91.93)×(-0.01)2×100]=8.84.

5、A bank has $100 million in assets with modified duration of 8.5, and $90 million of liabilities with modified duration of 6.5. Accounting only for duration effects, a 50 basis point parallel downward shift would impact the bank’s equity position by an amount closest to a:

A) $10 million increase in equity.  

B) $1.325 million increase in equity.

C) $100 million decrease in equity.  

D) $90 million increase in equity.

[此贴子已经被作者于2009-6-27 14:47:18编辑过]

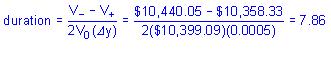
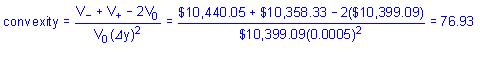
The correct answer is B

The change in assets would be an increase of ($100)(8.5)(0.005) = $4.25 million, whereas the change in liabilities would be an increase of ($90)(6.5)(0.005) = $2.925 million. The net effect would be an increase in equity of $1.325 million.

AIM 8: Compute the duration of a portfolio.

1、A bond portfolio consists of a AAA bond, a AA bond, and an A bond. The prices of the bonds are $1,050, $1,000, and $950 respectively. The durations are 8, 6, and 4 respectively. What is the duration of the portfolio?

A) 6.00.

B) 6.07.

C) 6.67.

D) 18.20.

[此贴子已经被作者于2009-6-27 14:48:08编辑过]

The correct answer is B

The duration of a bond portfolio is the weighted average of the durations of the bonds in the portfolio. The weights are the value of each bond divided by the value of the portfolio: portfolio duration = 8*(1050/3000)+6*(1000/3000)+4*(950/3000) = 2.8+2+1.27 = 6.07.

2、Suppose you have a two-security portfolio containing bonds A and B. The book value of bond A is $20 and the market value is $35. The book value of bond B is $40 and the market value is $50. The duration of bond A is 4.7 and the duration of bond B is 5.9. Which of the following amounts is closest to the duration of the portfolio?

A) 5.3.  

B) 5.5.

C) 5.4.  

D) 5.6.

The correct answer is C

Market values (not book values) should be used to calculate effective portfolio duration.

(35/85 × 4.7) + (50/85 × 5.9) = 5.41

3、Suppose you have a three-security portfolio containing bonds A, B and C. The effective portfolio duration is 5.9. The market values of bonds A, B and C are $60, $25 and $80, respectively. The durations of bonds A and C are 4.2 and 6.2, respectively. Which of the following amounts is closest to the duration of bond B?

A) 9.0.  

B) 1.4. 

C) 7.1.

D) 7.4.

The correct answer is A

Plug all the known figures and then solve for the one unknown figure, the duration of bond B.

Proof: (60/165 × 4.2) + (25/165 × 9.0) + (80/165 × 6.2) = 5.9

4、Which of the following statements about portfolio duration is FALSE? It is:

A) a measure of interest rate risk.  

B) a simple average of the duration estimates of the securities in the portfolio.

C) the weighted average of the duration estimates of the securities in the portfolio.  

D) measured using market prices of the bonds. 

The correct answer is B

Portfolio duration uses a weighted average figure, not a simple average.

AIM 9: Interpret the impact of changes in maturity, yield, and rating have on a bond’s duration.

1、Interest rate risk is most commonly associated with:

A) futures market. 

B) fixed income instruments. 

C) equity market. 

D) commodity market.  

The correct answer is B

Interest rate risk is most commonly associated with fixed income instruments or bonds. Futures, equity, and commodity markets are affected by interest rate risk only indirectly.

AIM 10: Explain the effect negative convexity has on hedging fixed income securities.

1、Positive convexity means that:

A) the graph of a callable bond flattens out as the market value approaches the call price.

B) the price of a fixed-coupon bond is inversely related to changes in interest rates.

C) bond price sensitivity is lowest when market yields are low.

D) as interest rates change, bond prices will increase at an increasing rate and decrease at a decreasing rate.

The correct answer is D

Positive convexity refers to the principle that for a given change in market yields, bond price sensitivity is lowest when market yields are high and highest when market yields are low.

Although the statements that begin, the graph of a callable bond . . . and the price of a fixed-coupon bond . . . are true, they are not the best choices to describe positive convexity.

2、Jayce Arnold, a CFA candidate, is studying how the market yield environment affects bond prices. She considers a $1,000 face value, option-free bond issued at par. Which of the following statements about the bond’s dollar price behavior is most likely accurate when yields rise and fall by 200 basis points, respectively? Price will:

A) increase by $124, price will decrease by $149.

B) decrease by $124, price will increase by $149.

C) decrease by $149, price will increase by $124.

D) increase by $149, price will decrease by $124.

The correct answer is B

As yields increase, bond prices fall, the price curve gets flatter, and changes in yield have a smaller effect on bond prices. As yields decrease, bond prices rise, the price curve gets steeper, and changes in yield have a larger effect on bond prices. Thus, the price increase when interest rates decline must be greater than the price decrease when interest rates rise (for the same basis point change). Remember that this applies to percentage changes as well.

3、Non-callable bond prices go up faster than they go down. This is referred to as:

A) inverse features.

B) negative convexity.

C) positive convexity.

D) embedded benefits.

The correct answer is C

When bond prices go up faster than they go down, it is called positive convexity.

4、Positive convexity in bond prices implies all but which of the following statements?

A) Bond prices approach a ceiling as interest rates fall.  

B) As yields increase, changes in yield have a smaller effect on bond prices. 

C) As yields decrease, changes in yield have a larger effect on bond prices.  

D) The price volatility of non-callable bonds is inversely related to the level of market yields.

The correct answer is A

The convexity of bond prices means that bond prices as a function of interest rates approach a floor as interest rates rise.

5、Convexity is important because:

A) the slope of the price yield curve is not linear.  

B) it measures the volatility of non-callable bonds. 

C) it can be used to indicate the optimal hedge ratio.  

D) the slope of the callable bond price/yield curve is backward bending at high interest rates.

The correct answer is A

Modified duration is a good approximation of price changes for an option-free bond only for relatively small changes in interest rates. As rate changes grow larger, the curvature of the bond price/yield relationship becomes more prevalent, meaning that a linear estimate of price changes will contain errors. The modified duration estimate is a linear estimate, as it assumes that the change is the same for each basis point change in required yield. The error in the estimate is due to the curvature of the actual price path. This is the degree of convexity. If we can generate a measure of this convexity, we can use this to improve our estimate of bond price changes.

6、Consider two bonds, A and B. Both bonds are presently selling at par. Each pays interest of $120 annually. Bond A will mature in 5 years while bond B will mature in 6 years. If the yields to maturity on the two bonds change from 12 percent to 10 percent, both bonds will:

A) increase in value, but bond B will increase more than bond A.

B) increase in value, but bond A will increase more than bond B.

C) decrease in value, but bond A will decrease more than bond B.

D) decrease in value, but bond B will decrease more than bond A.

The correct answer is A

There are three features that determine the magnitude of the bond price volatility:

(1) The lower the coupon, the greater the bond price volatility.

(2) The longer the term to maturity, the greater the price volatility.

(3) The lower the initial yield, the greater the price volatility.

Since both of these bonds are the same with the exception of the term to maturity, the bond with the longer term to maturity will have a greater price volatility.  Since bond value has an inverse relationship with interest rates, when interest rates decrease bond value increases. 

7、Which of the following bonds bears the greatest price impact if its yield declines by one percent? A bond with:

A) 30-year maturity and selling at 100.

B) 30-year maturity and selling at 70.

C) 10-year maturity and selling at 100.

D) 10-year maturity and selling at 70.

The correct answer is B

There are three features that determine the magnitude of duration:

(1) The lower the coupon, the greater the bond price volatility.

(2) The longer the term to maturity, the greater the price volatility.

(3) The lower the initial yield, the greater the price volatility.

The bond with the 30-year maturity will have a greater price impact than the 10-year maturity. The bond selling at the greatest discount will have a large price impact, a discount means that the coupon payments are low or the initial yield is low. So, the bond with the 30-year maturity and selling at 70 will have the greatest price volatility.

8、The convexity of a U.S Treasury bond is usually:

A) negative.

B) zero.

C) additional information is required.

D) positive.

The correct answer is D

One characteristic of all noncallable bonds is that they have positive convexity and U.S. Treasury bonds are noncallable bonds.