AIM 1: Compute, given the contractual rate and noninterest charges, the contractually promised gross return on a loan.

1、Given the following information:

Base lending rate = 6.0%

Risk premium = 1.2%

Origination fee = 0.25%

Compensating balance required = 10.0%

Reserve requirement = 12%

The contractually promised rate of return on a loan is closest to:

A) 7.49%.

B) 8.66%.

C) 9.05%.

D) 8.17%.

The correct answer is

The contractually promised return would be 8.17 percent, computed as follows:

2、Compensating balances represent the:

A) amount of commission that must be paid the underwriting banker.

B) proportion of a loan that must be kept on deposit at the financial institution that made the loan. 

C) ratio of interest to principal that measures risk in the asset-backed security industry.

D) amount of overcollateralization necessary to fund a special purpose entity (SPE).

The correct answer is B              

Compensating balances represent the proportion of a loan that borrowers cannot actively use for expenditures—it must be kept on deposit at the financial institution that made the loan.

3、Given the following information, compute the contractually promised rate of return on a loan. 

Base lending rate = 8.0% 

Risk premium = 2.0% 

Origination fee = 0.25% 

Compensating balance required = 12.50% 

Reserve requirement = 8% 

The contractually promised rate of return is closest to:

A) 17.5%.

B) 12.9%.

C) 13.7%.

D) 11.6%.

The correct answer is D

4、If the Federal Reserve wants to stimulate the economy by making loans more affordable, it could:

A) lower the prime rate.

B) sell securities in the open market.

C) reduce the risk premium.

D) lower the reserve requirement.

The correct answer is D

The Federal Reserve stimulates the economy by making more money available for loans as a result of lowering the reserve requirement. Although the Fed can influence the prime rate, it does not directly set it. The risk premium is independently determined by market participants.

5、If the Federal Reserve decreases the reserve requirement for a bank, the contractually promised rate of return on the loan would be:

A) the same.

B) lower.

C) higher or lower, depending on the level of short-term interest rates.

D) higher.

The correct answer is D

Decreasing the reserve requirement (r in the equation below) would mean that the bank had to keep fewer funds in reserve for a given loan, thus increasing the promised return (k).

6、The following information pertains to a loan:

Base lending rate = 5.0%.

Risk premium = 1.2%.

Origination fee = 0.25%.

Compensating balance required = 10.0%.

Reserve requirement = 15.0%.

The contractually promised rate of return on the loan is closest to:

A) 8.66%.

B) 9.05%.

C) 7.05%.

D) 6.28%. 

The correct answer is C

The contractually promised return would be 7.05%, computed as follows:

7、A loan has the following characteristics:

    ?  Base lending rate = 12%.

    ?  Risk premium = 3%.

    ?  Compensating balance requirement = 5%.

    ?  Loan origination fee = 0.5%.

    ?  Reserve requirement = 10%.

The contractually promised gross return on the loan is:

A) 16.23%.

B) 15.71%.

C) 16.67%. 

D) 20.94%.

The correct answer is

The promised rate of return on a loan, k, is determined using the following formula:

[attach]13899[/attach] 

where:

L     = the base lending rate

m    = the risk premium

f      = the loan origination fee

b     = the compensating balance requirement

R     = the reserve requirement

8、If a bank increases the percentage of compensating balances required for a loan, the contractually promised rate of return on the loan would be:

A) higher. 

B) not enough information. 

C) the same.

D) lower. 

The correct answer is A

Increasing the compensating balance would mean less cash investment for the bank, increasing the promised return.

9、If a borrower keeps less than the agreed compensating balance on deposit with the lending bank, the actual return to the lending bank on the loan will:

A) more than the promised yield.

B) still equal the promised rate.

C) be sold to a participating investor.

D) be less than the promised yield.

The correct answer is D

If a borrower keeps less on deposit than the agreed compensating balance, the bank will earn less on the loan than the promised return.

AIM 2: Analyze the relationship between the promised return and the expected return on a loan.

If the contractually promised rate of return on a loan is 8.5 percent and the probability of repayment is 98 percent, the expected return on the loan is closest to:

A) 6.88%.

B) 7.58%.

C) 6.33%. 

D) 8.33%.

The correct answer is C

The expected return includes the probability that the loan will be repaid:

AIM 4: Compute the cumulative default probability over a multiyear period given the marginal default probability for each year.

1、What is the probability that a corporate loan will be repaid if the 1-year T-bill rate is 8.0 percent and the rate on 1-year zero-coupon corporate bonds is 14.5 percent?

A) 94.32%.

B) 76.34%.

C) 93.50%.

D) 93.98%.

The correct answer is

The probability of repayment is:

 [attach]13901[/attach]

where:

p = probability of repayment

i = Treasury rates

k = corporate rates

So,

[attach]13902[/attach]

2、The risk-free rate on a 1-year Treasury bill (T-bill) is 3 percent and the implied probability of default on a 1-year zero-coupon corporate note is 3 percent, the promised rate of return on the corporate note is closest to:

A) 6.25%.

B) 6.50%.

C) 6.19%.

D) 6.77%.

The correct answer is C

The probability of default is defined as “1 – p”, and can be calculated with the following formula:

3、Basca, Inc. issued a 1-year zero-coupon note at a yield of 1.6 percent. The corresponding 1-year Treasury bill is yielding 1.04 percent. The implied probability of default on the Basca note is closest to:

A) 5.51%.

B) 5.54%.

C) 5.14%.

D) 0.55%.

The correct answer is D

The probability of default is defined as “1 – p,” and can be calculated with the following formula:

4、If the risk-free rate on a 1-year Treasury bill (T-bill) is 2.5 percent and the implied probability of default on a 1-year zero-coupon corporate note is 4.0 percent, the promised rate of return on the corporate note is closest to:

A) 6.50%.

B) 6.77%.

C) 6.25%.

D) 6.11%. 

The correct answer is B

The probability of default is defined as 1 – p, where p is implied probability of repayment and can be calculated with the following formula:

 [attach]13905[/attach]

where:

(1 – p) = probability of default

(1 + r) = the promised return on a risk-free investment

(1 + k) = the promised return on a risky investment

5、Atca Inc. issued a 1-year zero-coupon note at a yield of 6.8 percent. The corresponding 1-year Treasury bill (T-bill) is yielding 2.8 percent. The implied probability of default on the Atca note is closest to:

A) 3.75%.

B) 3.89%.

C) 3.96%. 

D) 0.37%.

The correct answer is A

The probability of default is defined as 1 – p, and can be calculated with the following formula:

6、Beta Inc. issued a 1-year zero-coupon note at a yield of 8.6 percent. The corresponding 1-year Treasury bill (T-bill) is yielding 8.2 percent. The implied probability of default on the Beta note is closest to:

A) 3.75%.

B) 0.37%. 

C) 3.89%. 

D) 3.96%.

The correct answer is Bfficeffice" />

The probability of default is defined as (1 – p) and can be calculated with the following formula:

7、Calculate the required risk premium for a one year corporate debt, if the one-year t-bill rate is 4%, the probability of repayment is 98%, and the recovery rate is 60%.

A) 0.85%.

B) 0.98%.

C) 1.17%.

D) 1.43%.

The correct answer is A

Φ = (1 + i) / (γ + p ? pγ) ? (1 + i) = (1.04) / (0.6 + 0.98 ? 0.588) ? 1.04 = 0.00838

AIM 5: Compute a marginal default probability using the term structure approach.

1、The cumulative probability of default for a note over two years is 3.8 percent. If the probability of default during the first year is 1.5 percent, the probability of default during the second year is closest to:

A) 2.96%.

B) 2.34%.

C) 3.17%.

D) 3.28%.

The correct answer is B

The cumulative probability of default is equal to one minus the probability of surviving to the end of the period without default:

2、The rate on a 1-year Treasury note (T-note) is 3.0 percent, and the rate on a 2-year T-note is 4.5 percent. The rate on a 1-year corporate note is 5 percent, and the rate on a 2-year corporate note is 6.8 percent. The implied probability of default on the corporate note in year two is closest to:

A) 2.34%.

B) 3.43%.

C) 2.40%.

D) 4.11%.

The correct answer is C

We can solve for the 1-year rate, one year forward for each of the T-notes and corporate bonds. Then we can use these two rates to determine the implied probability of default on the corporate note during the second year.

3、The marginal probability of default for years one and two is 0.5 percent and 1.1 percent, respectively. If the cumulative probability of default for the 3-year period is 4.45 percent, the marginal probability of default for year three is closest to:

A) 2.8%.

B) 2.9%.

C) 3.2%.

D) 2.7%.

The correct answer is B

The cumulative probability of default is equal to one minus the probability of surviving to the end of the period without default:

[attach]13911[/attach]

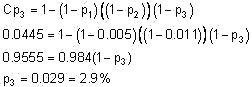
4、The rate on a 3-year Treasury note (T-note) is 3 percent, and the rate on a 4-year T-note is 4 percent, the rate on a 3-year corporate note is 5 percent and the rate on a 4-year corporate note is 6 percent. The implied cumulative probability of default on the corporate note in year 4 is closest to:

A) 0.94%.

B) 1.83%.

C) 1.91%.

D) 0.67%.

The correct answer is B

We can solve for the 1-year rate, three years forward for each of the T-notes and corporate bonds. Then, we can use these two rates to determine the implied probability of default on the corporate note during the fourth year.

5、The current one-year (zero) Treasury yield is 2.00 percent and the one-year yield on a firm’s debt is 2.37 percent. If it were estimated that on default the firm would pay 40 percent of the par value, what is the implied probability of default?

A) 0.375%.

B) 1.185%.

C) 2.370%.

D) 0.617%.

The correct answer is D

The equation for the 1-year probability of default is:

2.37% - 2.0% = (C1) (1-.40)

C1 = 0.6167%

6、The rate on a 1-year Treasury note (T-note) is 3.0 percent, and the rate on a 2-year T-note is 3.5 percent. The rate on a 1-year corporate note is 5 percent, and the rate on a 2-year corporate note is 6.8 percent. The implied probability of default on the corporate note in Year 2 is closest to:

A) 4.26%.

B) 2.96%.

C) 3.12%.

D) 4.21%.

The correct answer is A

We can solve for the 1-year rate and the 1-year forward for the T-note and corporate bond. Then, we can use these two rates to determine the implied probability of default on the corporate note during the second year:

7、The cumulative default rate for a cohort of bonds in the fifth year after rating is 2.25 percent, and the cumulative default rate for the sixth year is 2.52 percent. The marginal probability of default in the sixth year is closest to:

A) 2.39%.

B) 0.28%.

C) 96.25%. 

D) 0.24%.

The correct answer is B

The marginal default rate in the sixth year is: