AIM 2: Explain how the full valuation is supported by the Monte Carlo and historical simulation approach, respectively.

1、Local-valuation methods used to determine changes in portfolio value are appropriate when the portfolio:

A) has substantial option-like exposures.

B) has numerous complex risk factors.

C) has few option-like exposures.

D) changes are expected to occur over a long-term horizon.

The correct answer is C

Local-valuation methods are a first approximation to changes in overall portfolio value given changes in linear-related risk factors. The greater the nonlinear sensitivity of the portfolio (incurred by option-like exposures), or the more complex the sensitivity to risk factors, the less appropriate the application of the local-valuation method becomes.

AIM 3: List the advantages and disadvantages of using the delta-normal model, the historical simulation method, and the Monte Carlo simulation method for VAR calculations.

1、The delta-normal method is:

A) analytical. 

B) stochastic.

C) nonlinear.

D) called a Greek method.

The correct answer is A

The delta-normal method is analytical, because it describes VAR with a closed-form solution.

2、In a historical simulation method, the correlation among assets is:

A) embedded in the asset price changes.

B) ignored.

C) scaled by the gamma factor.

D) fixed at the current correlations.

The correct answer is A

In a historical simulation method, the correlation among assets is embedded in the asset price changes. One criticism of this method is that the correlations among assets are specific for the historical time period in which the prices were gathered and may vary for other periods.

AIM 4: Compare the delta normal, historical simulation, and Monte Carlo simulation methods, and explain their appropriate uses.

1、One advantage of the Monte Carlo simulation approach over the historical method when calculating VAR is the simulation approach:

A) makes better use of computing power.

B) takes advantage of the normal distribution.

C) equates past performance to future results.

D) incorporates flexibility in modeling price paths.

The correct answer is A 

The Monte Carlo approach allows for whatever relationships the VAR modeler would like to take into account. It is the most flexible method for generating VAR.

2、When would a Monte Carlo simulation be preferable to a historical simulation?

A) Historical data does not produce favorable results.

B) There is only a small amount of historical data.

C) Insufficient computer capacity.

D) A large amount of historical data is available.

The correct answer is B

Historical simulation is most applicable if there is a large sample of past returns to draw from. The computer capacity necessary for each is about the same, and certainly the occurrence of unfavorable results is no reason to reject historical simulation.

3、Many analysts prefer to use Monte Carlo simulation rather than historical simulation because:

A) it is much easier to generate the required variables.

B) past data is often proprietary and difficult to obtain. 

C) computers can manipulate theoretical data much more quickly than historical data.

D) past distributions cannot address changes in correlations or events that have not happened before.

The correct answer is D

While the past is often a good predictor of the future, simulations based on past distributions are limited to reflecting changes and events that actually occurred. Monte Carlo simulation can be used to model based on parameters that are not limited to past experience.

4、The difference between a Monte Carlo simulation and a historical simulation is that a historical simulation uses randomly selected variables from past distributions, while a Monte Carlo simulation:

A) uses a computer to generate random variables. 

B) uses randomly selected variables from future distributions.

C) uses variables based on roulette odds. 

D) projects variables based on a priori principles.

The correct answer is A

A Monte Carlo simulation uses a computer to generate random variables from specified distributions.

5、Which of the common methods of computing value at risk relies on the assumption of normality?

A) Variance/covariance.

B) Historical.

C) Monte Carlo simulation.

D) Rounding estimation.

The correct answer is A

The variance/covariance method relies on the assumption of normality.

6、Which value at risk methodology is most subject to model risk?

A) Parametric.

B) Variance/covariance.

C) Historical.

D) Monte Carlo simulation.

The correct answer is D

Monte Carlo simulation is subject to model risk.

7、Which of the following statements about value at risk (VAR) is TRUE?

A) VAR decreases with lower confidence level.

B) VAR decreases with longer holding periods.

C) VAR is not dependent on the choice of holding period.

D) VAR is independent of probability level.

The correct answer is A

VAR measures the amount of loss in the left tail of the distribution and increases with lower probability levels. Conversely VAR decreases with lower confidence levels (which is 1 minus the probability level). VAR actually increases with increases in holding period.

8、For a $1,000,000 stock portfolio with an expected return of 12 percent and an annual standard deviation of 15 percent, what is the VAR with 95 percent confidence level?

A) $120,000.

B) $150,000.

C) $127,500.

D) $247,500.

The correct answer is C

VAR = Portfolio Value[E(R)-zσ]= 1,000,000[0.12 – (1.65)(0.15)] = -$127,500

9、A portfolio comprises 2 stocks: A and B. The correlation of returns of stocks A and B is 0.8. Based on the information below, compute the portfolio’s annual VAR at a 5 percent probability level.

A) $10,295.

B) $11,700.

C) $13,300.

D) $23,491.

The correct answer is A

Weight of stock A = WA=0.75; Weight of stock B = WB = 0.25

Expected Portfolio return = E(RP) = 0.75(12)+0.25(10.8) = 11.70%

Portfolio Standard deviation =

sP = [(WA)2(sA)2+ (WB)2(sB)2+2(WA)(WB)rABsAsB]0.5

= [(0.75)2(0.15)2+(0.25)2(0.10)2+2(0.75)(0.25)(0.8)(0.15)(0.10)]0.5

= (0.0178)0.5

= 13.33%

VAR = Portfolio value [E(R)-zs]

= 100,000[0.117 – (1.65)(0.1333)] = -$10,295

10、A portfolio comprises 2 stocks: A and B. The correlation of returns of stocks A and B is 0.4. Based on the information below, what is the portfolio’s value-at-risk (VAR) at a 5 percent probability level?

A) $1,410.

B) $13,300.

C) $11,784.

D) $23,491.

The correct answer is C

Weight of stock A = WA= 0.85; Weight of stock B = WB = 0.15

Expected Portfolio return = E(RP) = 0.85(15)+0.15(12) = 14.55%

Portfolio Standard deviation =

           sP = [(WA)2(sA)2+ (WB)2(sB)2+2(WA)(WB)rABsAsB]0.5

            = [(0.85)2(0.18)2+(0.15)2(0.10)2+2(0.85)(0.15)(0.4)(0.18)(0.10)]0.5

            = (0.02547)0.5

            = 15.96%

VAR = Portfolio value [E(R) - zs] 

            = 100,000[0.1455 – (1.65)(0.1596)] = -$11,784

11、Derivation Inc. has a portfolio of $100 MM. The expected return over one year is 6 percent, with a standard deviation of 8 percent. What is the VAR for this portfolio at the 99 percent confidence level?

A) $2.0 MM.

B) $7.2 MM.

C) $12.1 MM.

D) $12.6 MM.

The correct answer is D

VAR = $100 MM [0.06 – (2.326)(0.08)] = $12.608 MM

12、If the one-day value at risk of a portfolio is $50,000 at a 95 percent probability level, this means that we should expect that in one day out of:

A) 20 days, the portfolio will decline by $50,000 or less.

B) 20 days, the portfolio will decline by $50,000 or more. 

C) 95 days, the portfolio will lose $50,000.

D) 95 days, the portfolio will increase by $50,000 or more.

The correct answer is B

This means that 5 out of 100 (or one out of 20) days, the value of the portfolio will experience a loss of $50,000 or more.

13、Value at risk (VAR) is a benchmark associated with a given probability. The actual loss:

A) may be much greater. 

B) cannot exceed this amount. 

C) is expected to be the average of the expected return of the portfolio and VAR.

D) will have an inverse relationship with VAR.

The correct answer is A

VAR is a benchmark that gives an estimate of what magnitude of loss would not be unusual. The actual loss for any given time period can be much greater.

14、A global portfolio is comprised of European and Emerging market equities. The correlation of returns for the two sectors is 0.3. Based on the information below, what is the portfolio’s annual value at risk (VAR) at a 5 percent probability level?

A) $110,700.

B) $130,300.

C) $230,491.

D) $128,280.

The correct answer is D

Weight of European equities = W_A=0.80; Weight of Emerging = W_B = 0.20

Expected Portfolio return = E(R_P) = 0.8(9)+0.2(18) = 10.80%

Portfolio Standard deviation = 

 σ_P = [(W_A)²(σ_A)²+ (W_B)²(σ_B)²+2(W_A)(W_B)r_ABσ_Aσ_B]^0.5

    = [(0.8)²(0.15)²+(0.2)²(0.25)²+2(0.8)(0.2)(0.3)(0.15)(0.25)]^0.5

    = (0.0205)^0.5

    = 14.32%

VAR = Portfolio Value[E(R) - zσ]
    = 1,000,000[0.108 – (1.65)(0.1432)] = -$128,280.

15、Alto Steel’s pension plan has $250 million in assets with an expected return of 12 percent. The last thirty monthly returns are given below.

What is the 10 percent monthly probability VAR for Alto’s pension plan?

A) $1,200,000.

B) $3,000,000.

C) $1,950,000.

D) $36,125,850.

The correct answer is C

Sorted monthly returns (from low to high, in columns) are as follows:

The 10% lowest return is the 3rd value (3/30 = 0.10), which is -0.78%
Therefore 10% VAR for the portfolio = 0.0078*250,000,000 = 1,950,000

16、Super Hedge fund has $20 million in assets. The total return for the past 40 months is given below. What is the monthly value at risk (VAR) of the portfolio at a 5 percent probability level?

A) $6,852,000.

B) $7,200,000.

C) $9,000,000.

D) $16,725,000.

The correct answer is A

Sorted monthly returns (from low to high, in columns) are as follows:

The 5% lowest return is the 2^nd value (2/40 = 0.05), which is -34.26%%
Therefore 5% VAR for the portfolio = 0.3426*$20,000,000 = $6,852,000

17、Portfolio A has total assets of $14 million and an expected return of 12.50 percent. Historical VAR of the portfolio at 5 percent probability level is $2,400,000. What is the portfolio’s standard deviation?

A) 12.50%.

B) 14.65%.

C) 17.97%.

D) 15.75%.

The correct answer is C

VAR = Portfolio Value [E(R)-zσ] 
-2,400,000 = 14,000,000[0.125 – (1.65)(X)] 
-2,400,000 = 1,750,000 – 23,100,000(X)
X = 17.97%.
Note that VAR value is always negative.

18、The minimum amount of money that one could expect to lose with a given probability over a specific period of time is the definition of:

A) delta. 

B) the hedge ratio. 

C) value at risk (VAR). 

D) the coefficient of variation. 

The correct answer is C

This is an often-used definition of VAR.

19、The Westover Fund is a portfolio consisting of 42 percent fixed income investments and 58 percent equity investments. The manager of the Westover Fund recently estimated that the annual VAR(5 percent), assuming a 250-day year, for the entire portfolio was $1,367,000 based on the portfolio’s market value of $12,428,000 and a correlation coefficient between stocks and bonds of zero. If the annual loss in the equity position is only expected to exceed $1,153,000 5 percent of the time, then the daily expected loss in the bond position that will be exceeded 5 percent of the time is closest to:

A) $72,623. 

B) $55,171. 

C) $46,445. 

D) $21,163.

The correct answer is C

Begin by using the formula for dollar portfolio VAR to compute the annual VAR(5%) for the bond position:

VAR2portfolio = VAR2Stocks + VAR2Bonds + 2VARStocksVARBonds ρStocks, Bonds

(1,367,000)2 = (1,153,000)2 + VAR2Bonds + 2(1,153,000)VARBonds(0)

VARBonds = [(1,367,000)2 – (1,153,000)2]0.5 = 734,357

Next convert the annual $VARBonds to daily $VARBonds:

734,357 / (250)0.5 = 46,445

20 Hugo Nelson is preparing a presentation on the attributes of value at risk. Which of Nelson’s following statements is not correct?

A) VAR can account for the diversified holdings of a financial institution, reducing capital requirements.

B) VAR(10%) = $0 indicates a positive dollar return is likely to occur on 90 out of 100 days.

C) VAR was developed in order to more closely represent the economic capital necessary to ensure commercial bank solvency.

D) VAR(1%) can be interpreted as the number of days that a loss in portfolio value will exceed 1%.

The correct answer is D

VAR is defined as the dollar or percentage loss in portfolio value that will be exceeded only X% of the time. VAR(10%) = $0 indicates that there is a 10% probability that on any given day the dollar loss will be greater than $0. Alternatively, we can say there is a 90% probability that on any given day the dollar gain will be greater than $0. VAR was developed by commercial banks to provide a more accurate measure of their economic capital requirements, taking into account the effects of diversification.

21、A large bank currently has a security portfolio with a market value of $145 million. The daily returns on the bank’s portfolio are normally distributed with 80% of the distribution lying within 1.28 standard deviations above and below the mean and 90% of the distribution lying within 1.65 standard deviations above and below the mean. Assuming the standard deviation of the bank’s portfolio returns is 1.2%, calculate the VAR(5%) on a one-day basis.

A) $2.87 million.

B) $2.23 million.

C) $2.04 million.

D) cannot be determined from information given.

The correct answer is A

VAR(5%) = z5% × σ × portfolio value

                   = 1.65 × 0.012 × $145 million

                   = $2.871 million

22、The accuracy of a value at risk (VAR) measure:

A) is included in the statistic.

B) can only be ascertained after the fact. 

C) is complete because the process is deterministic. 

D) is one minus the probability level. 

The correct answer is B

This is a weakness of VAR. The reliability can only be known after some time has passed to see if the number and size of the losses is congruent with the VAR measure.

23、A portfolio manager determines that his portfolio has an expected return of $20,000 and a standard deviation of $45,000. Given a 95 percent confidence level, what is the portfolio's VAR?

A) $43,500.

B) $54,250.

C) $74,250.

D) $94,250.

The correct answer is B

The expected outcome is $20,000. Given the standard deviation of $45,000 and a z-score of 1.65 (95% confidence level for a one-tailed test), the VAR is –54,250 [=20,000 – 1.65 (45,000)].

24、A $2 million balanced portfolio is comprised of 40 percent stocks and 60 percent intermediate bonds. For the next year, the expected return on the stock component is 9 percent and the expected return on the bond component is 6 percent. The standard deviation of the stock component is 18 percent and the standard deviation of the bond component is 8 percent. What is the annual VAR for the portfolio at a 1 percent probability level if the correlation between the stock and the bond component is 0.25?

A) $126,768.

B) $149,500.

C) $303,360.

D) $152,250.

The correct answer is C

Weight of Stock = WS=0.40; Weight of Bonds = WB = 0.60

Expected Portfolio return = E(RP) = 0.40(9)+0.60(6) = 7.20%

Portfolio Standard deviation =

σP = [(WS)2(σS)2+ (WB)2(σB)2+2(WS)(WB)rSBσSσB]0.5

= [(0.40)2(0.18)2+(0.60)2(0.08)2+2(0.40)(0.60)(0.25)(0.18)(0.08)]0.5

= (0.009216)0.5

= 9.6%

VAR = Portfolio Value [ E(R) -zσ]

= 2,000,000[0.072 – (2.33)(0.096)] = $303,360.

25、The price value of a basis point (PVBP) of a $20 million bond portfolio is $25,000. Interest rate changes over the next one year are summarized below:

Compute VAR for the bond portfolio at 95 percent confidence level.

A) $5,000,000.

B) $2,500,000.

C) $2,750,000.

D) $12,500.

The correct answer is A

At 5% probability level change in interest rates is 2.00% or higher.
Change in Portfolio value for 200 bps change in interest rate = 200*$25,000
VAR = $5,000,000.

26、Which of the following statements about value at risk (VAR) is TRUE?

A) VAR increases with longer holding periods.

B) VAR decreases with lower probability levels.

C) VAR is not dependent on the choice of holding period.

D) VAR is independent of probability level.

The correct answer is A

VAR measures the amount of loss in the left tail of the distribution. It increases with lower probability levels and increases in holding period.

27、Tim Jones is evaluating two mutual funds for an investment of $100,000. Mutual fund A has $20,000,000 in assets, an annual expected return of 14 percent, and an annual standard deviation of 19 percent. Mutual fund B has $8,000,000 in assets, an annual expected return of 12 percent, and an annual standard deviation of 16.5 percent. What is the daily value at risk (VAR) of Jones’ portfolio at a 5 percent probability if he invests his money in mutual fund A?

A) $1,668.

B) $1,924.

C) $13,344.

D) $38,480.

The correct answer is B

Daily standard deviation for mutual fund A = 0.19/√250= 0.012

Daily return = 0.14/250 = 0.00056

VAR = Portfolio Value [E(R)-zσ]

= 100,000[0.00056 – (1.65)(0.012)] = -$1,924.

28、If the expected change in a fixed income portfolio is $520,000 and the standard deviation of the estimated change in the portfolio is $2,275,500, the 95 percent value-at-risk (VAR) for this portfolio is closest to:

A) $855,400.00.

B) $3,743,197.50.

C) $3,223,197.50.

D) $4,598,597.50.

The correct answer is C

VAR for this portfolio would be –[$520,000 – 1.645($2,275,500)] = $3,223,197.50.

29、A hedge fund portfolio has an expected return of 0.1 percent per day and a 5 percent probability 1-day value at risk (VAR) of $909. Which of the following statement is the best descriptor of this information?

A) The maximum daily loss on the portfolio is $909.

B) The portfolio will earn more than $909 only 5% of the time.

C) The minimum daily loss on the portfolio is $909.

D) The minimum loss for the worst 5% of the days is $909.

The correct answer is C

By definition, VAR is the minimum loss for the worst 5% of the days or the maximum 1-day loss 95% of days. A minimum or maximum daily loss on the portfolio of $909 does not incorporate the alpha (probability). Alternatively, VAR can be stated in terms of confidence, e.g.

30、The price value of a basis point (PVBP) of a bond portfolio is $45,000. Expected changes in interest rates over the next year are summarized below:

What is the value at risk (VAR) for the bond portfolio at a 99 percent confidence level?

A) $2,250,000.

B) $6,750,000.

C) $4,500,000.

D) $7,850,500.

The correct answer is B

At 1% probability level change in interest rates is 1.50% or higher.
Change in Portfolio value for a 150 bps change in rates = 150*45000 = 6,750,000
VAR = 6,750,000.

31、The price value of a basis point (PVBP) of a bond portfolio is $45,000. Expected changes in interest rates over the next year are summarized below:

What is the value at risk (VAR) for the bond portfolio at a 99 percent confidence level?

A) $2,250,000.

B) $4,500,000.

C) $6,750,000.

D) $7,850,500.

The correct answer is C

At 1% probability level change in interest rates is 1.50% or higher.
Change in Portfolio value for a 150 bps change in rates = 150*45000 = 6,750,000
VAR = 6,750,000.

32、Which of the following statements about value at risk (VAR) is TRUE?

A) VAR increases with lower probability levels.

B) VAR decreases with longer holding periods.

C) VAR is not dependent on the choice of holding period.

D) VAR is independent of probability level.

The correct answer is A

VAR measures the amount of loss in the left tail of the distribution and increases with lower probability levels. VAR actually increases with increases in holding period.

33、An investor has 60 percent of his $500,000 portfolio in Value fund and the remaining in Growth fund. The correlation of returns of the two funds is –0.20. Based on the information below, what is the portfolio’s VAR at a 5 percent probability level?

A) $26,768.

B) $49,824.

C) $17,635.

D) $82,368.

The correct answer is C

Weight of Value Fund = WV=0.60; Weight of Growth Fund = WG = 0.40

Expected Portfolio return = E(RP) = 0.60(12)+0.40(16) = 13.60%

Portfolio Standard deviation =

σP = [(WV)2(σV)2+ (WG)2(σG)2+2(WV)(WG)rVGσVσG]0.5

= [(0.60)2(0.14)2+(0.40)2(0.20)2+2(0.60)(0.40)(-0.2)(0.14)(0.20)]0.5

= (0.010768)0.5

= 10.38%

VAR = Portfolio Value [ E(R) -zσ]

= 500,000[0.1360 – (1.65)(0.1038)] = -$17,635.

34、Kiera Reed is a portfolio manager for BCG Investments. Reed manages a $140,000,000 portfolio consisting of 30 percent European stocks and 70 percent U.S. stocks. If the VAR(1%) of the European stocks is 1.93 percent, or $810,600, the VAR(1%) of U.S. stocks is 2.13 percent, or $2,087,400, and the correlation between European and U.S. stocks is 0.62, what is the portfolio VAR(1%) on a percentage and dollar basis?

A) 1.90% and $2.67 million.

B) 2.07% and $2.90 million.

C) 1.90% and $2.90 million.

D) 2.07% and $2.67 million.

The correct answer is A

VAR for the portfolio on a percentage and dollar basis is calculated as follows:

35、If a 10-day VAR is $15,000,000, the 250-day VAR, assuming no change in confidence level, would be:

A) $237,000,000.

B) $23,700,000. 

C) $7,500,000.

D) $75,000,000.

The correct answer is D

Just back out the 1-day VAR by dividing by the square root of 10 and then multiply by the square root of 250 to get the 250-day VAR.

Just back out the 1-day VAR by dividing by the square root of 10 and then multiply by the square root of 250 to get the 250-day VAR.

36、Communities Bank has a $17 million par position in a bond with the following characteristics:

The bond is a 7-year, zero-coupon bond.

The market value is $12,358,674.

The bond is trading at a yield to maturity of 4.6%.

The historical mean change in daily yield is 0.0%.

The standard deviation of the position is 1%.

The one-day VAR for this bond at the 95% confidence level is closest to:

A) $105,257.

B) $203,918. 

C) $260,654.

D) $339,487.

The correct answer is B

VAR is the market value of the position times the price volatility of the position times the confidence level, which in this case equals ($12,358,674) × (0.01) × (1.65) = $203,918.

The 10-day VAR on this bond is closest to:

A) $866,111.

B) $644,845

C) $736,487.

D) $487,698.

The correct answer is B

The VAR is calculated as the daily earnings at risk times the square root of days desired, which is 10. The calculation generates ($203,918)(√10) = $644,845.

37、If a 1-day 95 percent VAR is $5 million, the 250-day 99 percent VAR level would be closest to:

A) $55.89 million.

B) $83.84 million.

C) $111.79 million.

D) $21.00 million.

The correct answer is C

First it is necessary to adjust for confidence levels (2.326/1.645), then by days (√250). In this case, ($5 million)(2.326/1.645)(√250) = $111.79 million.

38、The relationship between a three month call option and its underlying stock are presented in the following table.

Using the linear derivative VAR method and the information in the above table, what is a five percent VAR for the call option’s weekly return?

A) 10.8%.

B) 40.9%.

C) 15.8%.

D) 21.3%.

The correct answer is B

The weekly volatility is approximately equal to 2.08 percent a week (). The 5 percent VAR for the stock price is equivalent to a one standard deviation move, or 1.65 for the normal curve. The 5 percent VAR of the underlying stock is 0 – 2.08%(1.65)= –3.432%. A one percent change in the stock price results in a 11.92 percent change in the call option value, therefore, the delta = 0.1192/0.01 = 11.92. For small moves, delta can be used to estimate the change in the derivative given the VAR for the underlying asset as follows: VARCall = ΔVARStock =11.92(3.432%) = 0.409 or 40.9%. In words, the 5 percent VAR implies there is a 5 percent probability that the call option value will decline by 40.9% or more.

Using the linear derivative VAR method and the information in the table, and assuming 255 trading days in a year, what is a 1-percent VAR for the call option’s daily return?

A) 11.9%.

B) 15.8%.

C) 43.4%.

D) 26.1%.

The correct answer is D

The daily volatility is approximately equal to 0.94 percent a day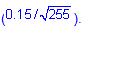The 1 percent VAR for the stock price is equivalent to a two standard deviation move, or 2.33 for the normal curve. The 1 percent VAR of the underlying stock is 0 – 0.94%(2.33) = 2.19%. A one percent change in the stock price results in a 11.92 percent change in the call option value, therefore, the delta = 0.1192/0.01 = 11.92. For small moves, delta can be used to estimate the change in the derivative given the VAR for the underlying asset as follows: VAR_Call = ΔVAR_Stock = 11.92(2.19%) = 0.261 or 26.1%. In words, the 1 percent VAR implies there is a 1 percent probability that the call option value will decline by 26.1% or more.

39、The most important way in which the Monte Carlo approach to estimating operational VAR differs from the historical method and variance-covariance method is:

A) its heavy dependence on historical data.

B) it involves repeatedly shocking a model of risk data to produce a range of potential losses.

C) its computational simplicity. 

D) its inability to account for non-linear risk structures. 

The correct answer is B

The Monte Carlo approach uses simulation techniques, repeatedly shocking a model of loss data in order to produce a range of potential losses. It is more computationally intensive than either the historical or variance-covariance approaches. The model used can account for nonlinear risk structures and need not be limited by historical data.

40、The VaR measure obtained from simulating data based on assumptions concerning the return distributions is called:

A) Prospective VaR.

B) Stochastic VaR. 

C) Monte Carlo VaR.

D) Kurtotic VaR. 

The correct answer is C

Monte Carlo VaR uses data generated from a simulation procedure.

41、Which of the following statements comparing Monte Carlo VaR and historical VaR is most accurate?

A) Both compute VaR from percentiles from a given set of observed returns, but Monte Carlo VaR uses realized returns and historical VaR uses hypothetical returns.

B) Both are parametric approaches, but historical VaR uses a regression on past data while Monte Carlo VaR uses Kalman filtering to create forward looking VaR estimates. 

C) Both are parametric approaches, but Monte Carlo VaR uses fewer inputs into the model than historical VaR.

D) Both compute VaR from percentiles from a given set of observed returns, but historical VaR uses realized returns and Monte Carlo VaR uses hypothetical returns.

The correct answer is D

Historical VaR uses historical realized returns, and Monte Carlo VaR uses returns generated from a hypothetical model, which requires a significant number of inputs. Neither historical nor Monte Carlo VaR is a parametric approach.

42、On December 31, 2006, Portfolio A had a market value of $2,520,000. The historical standard deviation of daily returns was 1.7%. Assuming that Portfolio A is normally distributed, calculate the daily VAR(2.5%) on a dollar basis and state its interpretation. Daily VAR(2.5%) is equal to:

A) $83,966, implying that daily portfolio losses will fall short of this amount 2.5% of the time.

B) $70,686, implying that daily portfolio losses will only exceed this amount 2.5% of the time.

C) $70,686, implying that daily portfolio losses will fall short of this amount 2.5% of the time.

D) $83,966, implying that daily portfolio losses will only exceed this amount 2.5% of the time.

The correct answer is D

VAR(2.5%)Percentage Basis = z2.5% × σ = 1.96(0.017) = 0.03332 = 3.332%.

VAR(2.5%)Dollar Basis = VAR(2.5%)Percentage Basis × portfolio value = 0.03332 × $2,520,000 $83,966.

The appropriate interpretation is that on any given day, there is a 2.5% chance that the porfolio will experience a loss greater than $83,996. Alternatively, we can state that there is a 97.5% chance that on any given day, the observed loss will be less than $83,996.

43、You wish to estimate VAR using a local valuation method. Which of the following are methods you might use?

Historical simulation.

The delta-normal valuation method.

Monte Carlo simulation.

The grid Monte Carlo approach.

A) II only.

B) I only.

C) I and II only.

D) III and IV only.

The correct answer is A

Local valuation methods measure portfolio risk by valuing the assets at one point in time, then making adjustments to relevant risk factors that are expected to cause changes in the overall portfolio value. The delta-normal valuation method is an example of a local valuation method.

44、

Suppose that the stock price is currently at $25.00 and the 3-month call option with an exercise price of $24.00 is $1.60. Using the linear derivative VAR method and the information in the above table, what is a 5% VAR for the call option’s weekly return?

 A) 50.7%.

B) 43.4%.

C) 21.6%.

D) 45.3%.

The correct answer is D

 The weekly volatility is approximately equal to 2.77% a week (0.20 / √52). The 5% VAR for the stock price is equivalent to a 1.65 standard deviation move for a normal curve. The 5% VAR of the underlying stock is 0 ? 2.77%(1.65) = ?4.57%. A ?1% change in the stock price results in a 9.91% change in the call option value, therefore, the delta = ?0.0991 / ?0.01 = 9.91. For small moves, delta can be used to estimate the change in the derivative given the VAR for the underlying asset as follows: VARCall = ΔVARStock = 9.91(4.57%) = 0.4529, or 45.29%. In words, the 5% VAR implies there is a 5% probability that the call option value will decline by 45.29% or more over one week.

45、

Alton Richard is a risk manager for a financial services conglomerate. Richard generally calculates the VAR of the company’s equity portfolio on a daily basis, but has been asked to estimate the VAR on a weekly basis assuming five trading days in a week. If the equity portfolio has a daily standard deviation of returns equal to 0.65% and the portfolio value is $2 million, the weekly dollar VAR (5%) is closest to:

A) $29,100.

B) $21,450.

C) $107,250.

D) $47,964.

The correct answer is D

The weekly VAR is 2 million × 1.65 × 0.0065 × √5 = $47,964.