

1.Using the following tree of semiannual interest rates what is the value of a putable semiannual bond that has one year remaining to maturity, a put price of 98 and a 4 percent coupon rate? The bond is putable today.
7.59%
6.35%
5.33%
A) 98.75.
B) 97.92.
C) 98.00.
D) 99.52.
2.Which of the following is the appropriate "nodal decision" within the backward induction methodology of the interest tree framework for a putable bond?
A) Max(put price, discounted value).
B) Max(par value, discounted value).
C) Min(call price, discounted value).
D) Min(put value, discounted value).
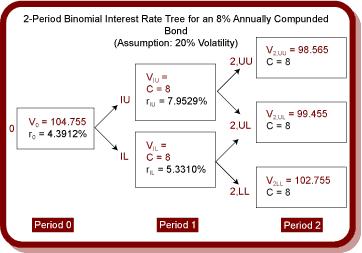
3.Dawn Adams, CFA, along with her recently hired staff, have responsibilities that require them to be familiar with backward induction methodology as it is used with a binomial valuation model. Adams, however, is concerned that some of her staff, particularly those not enrolled in the CFA program, are a little weak in this area. To assess their understanding of the binomial model and its uses, Adams presented her staff with the first two years of the binomial interest rate tree for an 8% annually compounded bond (shown below). The forward rates and the corresponding values shown in this tree are based on an assumed interest rate volatility of 20%.

A member of Adams' staff has been asked to respond to the following:
Compute V
A) $103.58.
B) $95.99.
C) $99.01.
D) $101.05.
4.Compute V1U, the value of the bond at node 1U.
A) $99.01.
B) $99.13.
C) $91.72.
D) $101.11.
5.Compute V0, the value of the bond at node 0.
A) $99.07.
B) $101.35.
C) $104.76.
D) $105.70.

1.Using the following tree of semiannual interest rates what is the value of a putable semiannual bond that has one year remaining to maturity, a put price of 98 and a 4 percent coupon rate? The bond is putable today.
7.59%
6.35%
5.33%
A) 98.75.
B) 97.92.
C) 98.00.
D) 99.52.
The correct answer was C)
The putable bond price tree is as follows:
| 100.00 | |
A ==> 98.27 |
| |
98.00 |
| 100.00 |
| 99.35 | |
| 100.00 | |
| | |
As an example, the price at node A is obtained as follows:
PriceA = max{(prob * (Pup + coupon/2) + prob * (Pdown + coupon/2))/(1 + rate/2), putl price} = max{(0.5 * (100 + 2) + 0.5 * (100 + 2))/(1 + 0.0759/2),98} = 98.27. The bond values at the other nodes are obtained in the same way.
The price at node 0 = [.5*(98.27+2) + .5*(99.35+2)]/ (1 + 0.0635/2) = $97.71 but since this is less than the put price of $98 the bond price will be $98.
2.Which of the following is the appropriate "nodal decision" within the backward induction methodology of the interest tree framework for a putable bond?
A) Max(put price, discounted value).
B) Max(par value, discounted value).
C) Min(call price, discounted value).
D) Min(put value, discounted value).
The correct answer was A)
When valuing a putable bond using the backward induction methodology, the relevant cash flow to use at each nodal period is the coupon to be received during that nodal period plus the computed value or exercise price, whichever is greater.
3.Dawn Adams, CFA, along with her recently hired staff, have responsibilities that require them to be familiar with backward induction methodology as it is used with a binomial valuation model.

A member of
Compute V
A) $103.58.
B) $95.99.
C) $99.01.
D) $101.05.
The correct answer was A)
V
V
4.Compute V1U, the value of the bond at node 1U.
A) $99.01.
B) $99.13.
C) $91.72.
D) $101.11.
The correct answer was B)
V1U = (½)[(V2,UU + C) / (1 + r1U)] + [(V2,UL + C)/(1 + r1U)]
V1U = (½)[(98.565 + 8) / (1 + 0.079529)] + [(99.455 + 8) / (1 + 0.079529)] = $99.127
5.Compute V0, the value of the bond at node 0.
A) $99.07.
B) $101.35.
C) $104.76.
D) $105.70.
The correct answer was C)
V0 = (½)[(V1U + C) / (1 + r0)] + [(V
From the previous question the value for V1U was determined to be $99.127
V0 = (½)[(99.127 + 8) / (1 + 0.043912)] + [(103.583 + 8)/(1 + 0.043912)] = $104.755
| 欢迎光临 CFA论坛 (http://forum.theanalystspace.com/) | Powered by Discuz! 7.2 |