Question 7 - 9675
   

Dawn Adams, CFA, along with her recently hired staff, have responsibilities that require them to be familiar with backward induction methodology as it is used with a binomial valuation model. Adams , however, is concerned that some of her staff, particularly those not enrolled in the CFA program, are a little weak in this area. To assess their understanding of the binomial model and its uses, Adams presented her staff with the first two years of the binomial interest rate tree for an 8 percent annually compounded bond (shown below). The forward rates and the corresponding values shown in this tree are based on an assumed interest rate volatility of 20 percent.

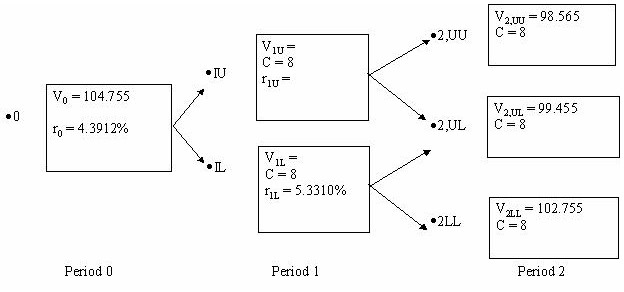
2-Period Binomial Interest Rate Tree for an 8% Annually Compounded Bond

(Assumption: 20% Volatility)

A member of Adams' staff has been asked to respond to the following:

Part 1)
Compute V_1L, the value of the bond at node 1L.

Part 2)
What is the value of r_1U, the one-year forward rate at the upper node at period 1?

Part 3)
Compute V_1U, the value of the bond at node 1U.

Part 4)
Compute V₀, the value of the bond at node 0.

Part 5)
Assume that the bond is putable in one year at par ($100) and that the put will be exercised if the computed value is less than par. What is the value of the putable bond?

Part 6)
Assume that the bond is putable in one year at par ($100) and that the put will be exercised if the computed value is less than par. What is the value of the put option?

[此贴子已经被作者于2007-5-13 16:26:07编辑过]

Question

Part 1)
Your answer: B was incorrect. The correct answer was A) $103.58.

V_1L = ½[(V_2LU + C)/(1 + r_1L) + (V_2LL + C)/(1 + r_1L)]

V_1L = ½[(99.455 + 8)/(1 + 0.05331) + (102.755+ 8)/(1 + 0.05331)] = $103.583

Part 2)
Your answer: B was incorrect. The correct answer was A) 7.953%.

r_1U = (5.331)e^2(.2) = 7.9529%

Part 3)
Your answer: B was incorrect. The correct answer was A) $99.13.

V_1U = ½[(V_2,UU+ C)/(1 + r_1U) + (V_2,UL + C)/(1 + r_1U)]

From the previous question the value for r_1U was determined to be 7.9529%. Using this value for the forward rate:

V_1L = ½[(98.565 + 8)/(1 + 0.079529) + (99.455 + 8)/(1 + 0.079529)] = $99.127

Part 4)
Your answer: B was incorrect. The correct answer was C) $104.76.

V₀ = ½[(V_1U + C)/(1 + r₀) + (V_1L + C)/(1 + r₀)]

From the previous question the value for V_1U was determined to be $99.127

V₀ = ½[(99.127 + 8)/(1 + 0.043912) + (103.583+ 8)/(1 + 0.043912)] = $104.755

Part 5)
Your answer: B was correct!

The relevant value to be discounted using a binomial model and backward induction methodology for a putable bond is the value that will be received if the put option is exercised or the computed value, whichever is greater.

In this case, the relevant value at node 1U is the exercise price ($100.000) since it is greater than the computed value of $99.127. At node 1L, the computed value of $103.583 must be used.

Therefore, the value of the putable bond is:

V₀ = ½[(100.00 + 8)/(1 + 0.043912) + (103.583+ 8)/(1 + 0.043912)] = $105.17314

Part 6)
Your answer: B was incorrect. The correct answer was A) $0.42.

V_putable = V_straight + V_put

Rearranging, the value of the put can be stated as:

V_put = V_putable - V_straight

V_putable was computed to be $105.173 in the previous question, and V_straight was determined to be $104.755 in the question prior to that. So the value of the embedded put option for the bond under analysis is:

$105.173 - 104.755 = $0.418